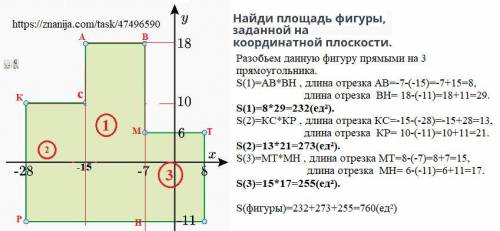
Найди площадь фигуры, заданной на координатной плоскости.
Объяснение:
Разобьем данную фигуру прямыми на 3 прямоугольника.
S(1)=АВ*ВН , длина отрезка АВ=-7-(-15)=-7+15=8,
длина отрезка ВН= 18-(-11)=18+11=29.
S(1)=8*29=232(ед²).
S(2)=КС*КР , длина отрезка КС=-15-(-28)=-15+28=13,
длина отрезка КР= 10-(-11)=10+11=21.
S(2)=13*21=273(ед²).
S(3)=МТ*МН , длина отрезка МТ=8-(-7)=8+7=15,
длина отрезка МН= 6-(-11)=6+11=17.
S(3)=15*17=255(ед²).
S(фигуры)=232+273+255=760(ед²)
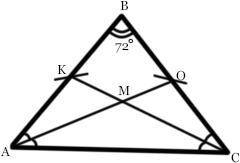
Дано :
ΔАВС - равнобедренный (АВ = ВС).
∠В = 72°.
Отрезок АО - биссектриса ∠А.
Отрезок СК - биссектриса ∠С.
Точка М - точка пересечения АО и СК.
Найти :
∠АМС = ?
Углы при основании равнобедренного треугольника равны.Следовательно -
∠А = ∠С.
Сумма внутренних углов треугольника равна 180° (теорема о сумме внутренних углов треугольника).Следовательно -
∠А + ∠В + ∠С = 180°
∠А + ∠С = 180° - ∠В
∠А + ∠С = 180° - 72°
∠А + ∠С = 108°
∠А = ∠С = 108° : 2 = 54°.
Биссектриса угла треугольника - это отрезок, который является биссектрисой угла треугольника.Отсюда -
∠КАМ = ∠МАС = 54° : 2 = 27°
∠АСМ = ∠МСО = 54° : 2 = 27°.
Рассмотрим ΔАМС.
По теореме о сумме внутренних углов треугольника -
∠МАС + ∠АСМ + ∠АМС = 180°
∠АМС = 180° - ∠МАС - ∠АСМ
∠АМС = 180° - 27° - 27°
∠АМС = 126°.
126°.
На стороне AC треунольника АВС выбрана точка Е так что AE:EC=5:4. В каком отношении ВЕ делит медиану АD.(ещё нужно провести прямую DK параллельную BE)
8 класс теорема фалеса
Объяснение: