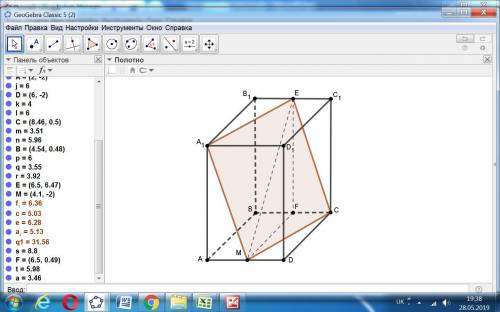
А) Так как сечение проходит через параллельные плоскости , то в сечении - параллелограмм.
Находим его стороны. А1Е = √(1 + (1/2)²) = √5/2.
А1М = √(3² + (1/2)²) = √37/2.
Найдём диагональ МЕ: МЕ =√(1² +3²) = √10.
Площадь параллелограмма найдём как площадь двух треугольников со сторонами, равными сторонам параллелограмма и его диагонали.
Площадь треугольника определяем по формуле Герона.
Треугольник А1ЕМ
a(ЕМ) b(А1М) c(А1Е) p 2p S
3,1623 3,0414 1,11803 3,6609 7,3217 1,6956
10 9,25 1,25 это квадраты сторон
cos A = 0,0735 cos B = 0,2828 cos С = 0,9358
Аrad = 1,4972 Brad = 1,2840 Сrad = 0,3603
Аgr = 85,7837 Bgr = 73,5700 Сgr = 20,6462 .
Площадь сечения равна 2*1,6956 = 3,3912 кв.ед.
Б) Перпендикуляр из точки F на МС равен (1*(1/2)/(√5/2) = 1/√5.
Тангенс угла α наклона плоскости сечения равен:
tg α = 3/(1/√5) = 3√5.
α = arc tg(3√5) = 1,4228 радиан или 81,5213 градуса.
треугольник АВС~А1В1С1( по условию)
Раз сторона А1В1 больше на 3,4 см значит А1В1=АВ+3,4=10,2
составляем соотношение:
А!В!А1=В1С1/В1=А1С1/АС=коэфициенту(к)
АВ/А1В1=к
АВ\А1В1= 10,2/6,8=1,5
В1С1/ВС=1,5: В1С1/3,2=4,8
А1С1/АС= 1,5 : А1С1/7,6=11,4