Сделаем рисунок к задаче.
Рассмотрим треугольники АКС и АЕС. Углы при К и Е в них равны, так как являются вписанными углами опирающимися на одну и ту же дугу, стягиваемую хордой АС.
Следовательно углы ВКС и ВЕА тоже равны как смежные с ними.
Угол КОЕ прямой по условию задачи.
Сумма углов четырехугольника равна 360°
Сумма равных углов ВКС и ВЕА равна
360-90-20=250°
Углы эти равны по 250:2=125°
Смежные с ними углы АЕС и АКС равны по 180-125= 55°
Сумма углов треугольника равна 180°
Так как угол ЕОС прямой, угол КСВ равен 180-90-55=35°
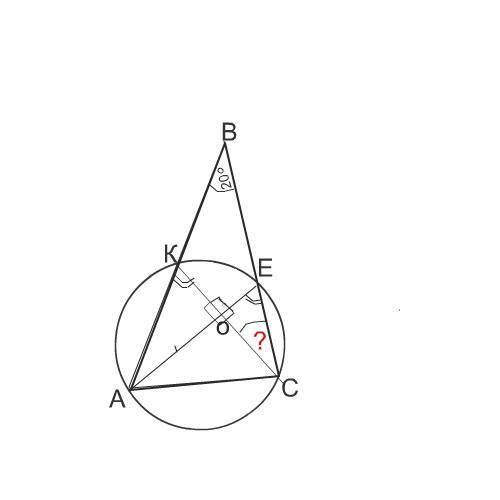
Сделаем рисунок к задаче.
Рассмотрим треугольники АКС и АЕС. Углы при К и Е в них равны, так как являются вписанными углами опирающимися на одну и ту же дугу, стягиваемую хордой АС.
Следовательно углы ВКС и ВЕА тоже равны как смежные с ними.
Угол КОЕ прямой по условию задачи.
Сумма углов четырехугольника равна 360°
Сумма равных углов ВКС и ВЕА равна
360-90-20=250°
Углы эти равны по 250:2=125°
Смежные с ними углы АЕС и АКС равны по 180-125= 55°
Сумма углов треугольника равна 180°
Так как угол ЕОС прямой, угол КСВ равен 180-90-55=35°

Даны вершины треугольника A(-3; 1), B(-1; 5), C(2; 5).
Основанием медианы из точки С является точка М как середина стороны АВ.
Находим координаты точки М.
М((-3-1)/2; (1+5)/2) = (-2; 3).
Вектор СМ = (-2-2; 3-5) = (-4; -2).
Уравнение СМ: (х - 2)/(-4) = (у - 5)/(-2).
Можно упростить, разделив знаменатели на (-2).
СМ: (х - 2)/2 = (у - 5)/1 или в общем виде х - 2у + 8 = 0.