геометрия (9 класс)
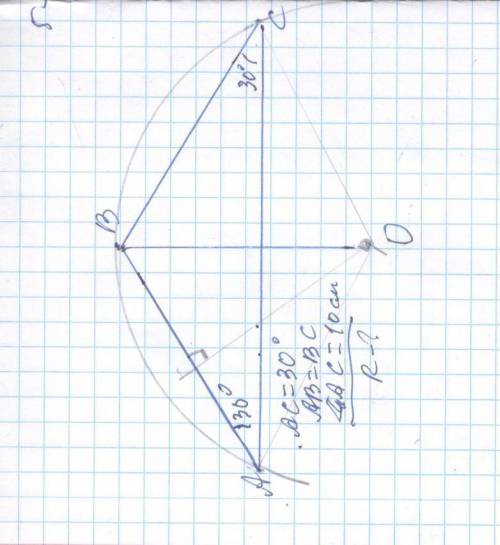
Найти длину окружности ,описанной около равнобедренного треугольника с основанием 10 см и углом 30° при основании .
Дано: ∠A = ∠C =30 ° , AC=b =10 см
----------------------------
R - ?
решение : Можно разными но геометрия (9 класс)
→ рационально использовать теорема синусов :
a/sin∠A = b /sin∠B = c /sin∠C = 2R
Угол против основания ∠B =180° - (30°+30°) = 180° - 60° 120°
AC/sin∠B =2R ⇔ R = AC/2sin∠B
R = 10 /2sin(180° - 60°) =10/2sin60° =10/ (2*√3 / 2) =10 /√3 =( 10√3) /3
пусть точка А находится внутри окружности, те расстояние от точки А до центра окружности меньше радиуса окружности.
и пусть через точку можно провести прямую так, чтобы она не являлась секущей, те имела с окружностью 1 или 0 точек пересечения. Но о точек перес прямая иметь не может тк имеется одна точка, принадлежащая прямой и находящаяся внутри окружности. Получаем 1 т перес. 1 т перес. с прямой это касательная, но касательная проходит через точку на окружности, следовательно тА лежит на окружности, следовательно расстояние от А до центра = радиусу, что противоречит условию. имеем 2 т пересечения.
240 палочек
Объяснение:
было всего минут их стало еще 20 минут и их стало уже 1 час и их стало 240