8+16√2 см²
Объяснение:
Дано:
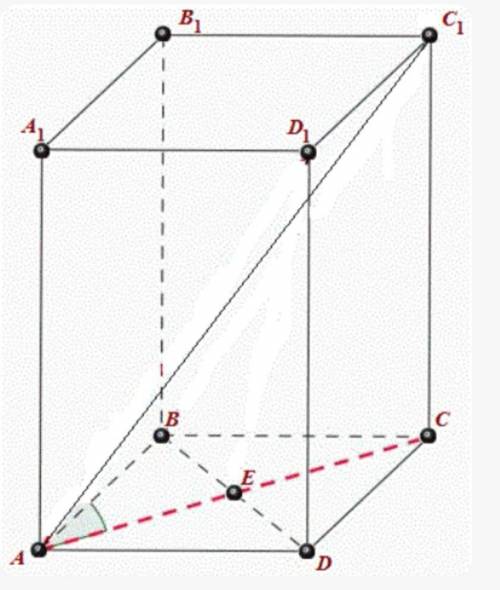
АВСDA1B1C1D1 призма.
АВСD- квадрат.
АС1=4см диагональ призмы.
АВ=ВС=СD=AD=2см
Sпол=?
Решение
Sпол=2Sосн+Sбок
Sосн=АВ²=2²=4 см² площадь квадрата.
АС- диагональ квадрата.
АС=АВ√2=2√2 см диагональ квадрата.
∆АС1С- прямоугольный.
АС1- гипотенуза.
АС и СС1 - катеты.
По теореме Пифагора найдем СС1
СС1=√(АС1²-АС²)=√(4²-(2√2)²)=√(16-8)=√8=
=2√2 см высота призмы.
Формула нахождения площади боковой поверхности призмы
Sбок=Росн.*h, где Росн.-периметр основания (квадрата); h=CC1.
Sбок=4*АВ*СС1=4*2*2√2=16√2 см² площадь боковой поверхности призмы.
Sпол.=2*Sосн.+Sбок=2*4+16√2=8+16√2 см² площадь полной поверхности призмы.
После построения рисунка поусловию задачи трапеция будет поделена на 2 прямоугольных равнобедренных подобных Δ ABC и Δ ACD из Δ ACD находим по Пифагору большее основание AD=√(16^2+16^2)=16√2.см
Из подобия Δ ABC и Δ ACD , получаем соотношение 16/16√2=BC/16 => BC=16/√2 см
Высота трапеции равна AB=16/√2 см
Средняя линия равна: (16/√2+16√2)/2=24 см
Периметр= (2*16/√2+16+16√2)=(48√2+16) см
Площадь S=24*16/√2=384/√2 см^2