
Сделаем рисунок к задаче.
Обозначим вершины параллеограмма привычными буквами АВСD.
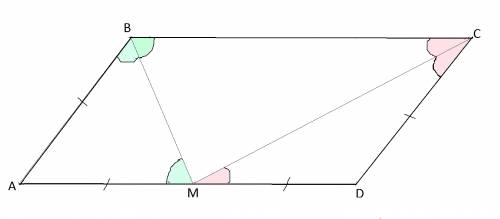
Проведем биссектрисы углов В и С, которые пересекутся на АD в точке М.
Биссектрисы образовали со сторонами параллелограмма треугольники, причем
∠ СВМ= ∠ АМВ по свойству углов при пересечении параллельных прямых и секущей, а
∠ АВМ= ∠МВС - как половины угла В.
То же самое с углами ВСМ и СМD.
Раз углы при основании ВМ Δ АВМ и основании СМ Δ СМD равны,
оба этих треугольника - равнобедренные.
В треугольнике АВМ сторона АВ равна стороне АМ,
В треугольнике МDС сторона МD равна стороне СD.
Но АВСD- параллелограмм, и стороны АВ и CD равны по определению.
Следовательно, АМ=MD и АD=2АВ ( или 2 CD, что одно и то же)
Р АВСD= 2( АВ+АD) Подставим в значение периметра 2 АВ вместо AD.
Р АВСD= 2( АВ+2АВ)
30= 6 АВ
АВ=5 см
Ответ: Длина короткой стороны параллелограмма равна 5 см
1) т.к. сумма углов треугольника=180*, то угол А=180-(82+40)=58*
2) т.к. СС1-биссектриса угла С, то угол С1СВ и угол С1СА=20*
3) т.к. АА1-биссектриса угла А, то угол ВАА1 и угол А1АС=29*
4) т.к. сумма углов треугольника=180*, то угол ВС1С=180-(82+20)=78*
5) т.к. сумма углов треугольника=180*, то угол ВА1А=180-(82+29)=69*
6) из 2 пункта следует, что угол С1СА=20*
из 3 пункта следует, что угол А1АС=29*
7) т.к. сумма углов треугольника=180*, то из 6 пункта следует, что угол АМС=180-(29+20)=131*
8) т.к. угол АМС и угол С1МА1 вертикальные, следовательно они равны, следовательно угол С1МА1=131*
Или так:1) угол С1СА=40:2=20
уголМАС=(180-82-40):2=29
уголС1МА1=углуАМС=180-20-29=131
2)угол ВС1С=180-20-82=78
3)угол ВА1М=360-78-131-82=69
ответ:короче...
S=Пr^2
если п=3, то s=3*2*2=12... но нам нужна не вся площадь круга.. а только половина.. тобишь будет 12/2=6...
теперь находим площадь самой фигуры у которой прорисован радиус.. он равен 8... а нам нужна только 8-6=2...
за тем находим такую шнягу у всех фигур с радиусами... она равна 2*4=8...
теперь находим площадь прямоугольника.. она равна 3*8=24...
ну и наконец то находим площадь нужной фигуры.. она равна 24+8=32
Объяснение:Надеюсь