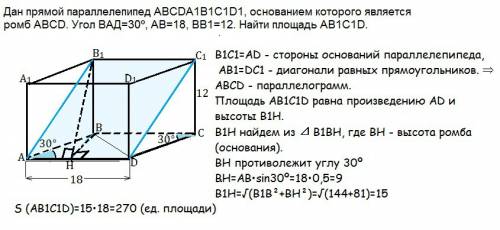
Дан прямой параллелепипед АВСDА1В1С1D1, основанием которого является ромб АВСD. Угол ВАD=30º, АВ=18, ВВ1=12.
Найти площадь AB1C1D.
––––––––––
В прямом параллелепипеде все ребра перпендикулярны основанию, а грани - прямоугольники.
В четырехугольнике AB1C1D стороны В1С1и АD равны как стороны оснований параллелепипеда,
АВ1=DС1 - диагонали равных прямоугольников. ⇒
АВ1С1D - параллело1грамм,т.к. его противоположные стороны равны и параллельны.
Площадь AB1C1D равна произведению АD и высоты, проведенной к АD.
Высота ромба BH - проекция наклонной В1Н на плоскость ромба.
ВН ⊥ АD ⇒
по теореме о 3-х перпендикулярах В1Н⊥ АD и является высотой АВ!С1D
По т.Пифагора из ⊿ В1ВН
B1H=√(B1B²+BH²)
В ромбе высота ВН противолежит углу ВАD=30º
ВН=АВ*sin30º=18*0,5=9
B1H=√(144+81)=15
S (AB1C1D)=15•18=270 (ед. площади)
Объяснение:
Противоположные углы в параллелограме равны между собой.
Углы прилежащие к одной стороне равны 180°
а)
Пусть градусная мера одного угла будет х, тогда другого будет х+40.
Составляем уравнение.
х+(х+40)=180
2х=180-40
2х=140
х=140/2
х=70° градусная мера одного угла.
Градусная мера второго угла х+40, подставляем значение х.
70+40=110°
ответ: углы в параллелограме равны 40°;110°;40°;110°
б)
Пусть градусная мера одного угла будет х, тогда градусная мера второго угла будет 5х.
Составляем уравнение.
х+5х=180°
6х=180
х=180/6
х=30° градусная мера одного угла.
Градусная мера второго угла 5х, подставляем значение х.
5*30=150° градусная мера второго угла.
ответ: градусные меры углов в параллелограме равны: 30°; 150°; 30°;150°
Из формулы объема шара V=4/3ПR^3 находим радиусы обоих шаров
2= 4/3ПR^3 3= 4/3ПR^3
6= 4ПR^3 9= 4ПR^3
R^3 =6/ (4П) R^3 =9/ (4П)
R1=кубический корень из 6/ (4П ) R2=кубический корень из 9/ (4П)
Находим площади поверхности каждого шара S=4 ПR^2
S1= 4 П*( кубический корень из 6/ (4П ) ^2 = 4 П * кубический корень из 36/(16П^2)
S2= 4 П*( кубический корень из 9/ (4П ) ^2 = 4 П * кубический корень из 81/(16П^2)
Находим отношение
S1 4 П*( кубический корень из 6/ (4П ) ^2 = 4 П * кубический корень из 36/(16П^2)
__ =
S2 4 П*( кубический корень из 9/ (4П ) ^2 = 4 П * кубический корень из 81/(16П^2)
= кубический корень из ( 36/ 81)= кубический корень из ( 4/ 9)
(Стопроцентность решения не гарантирую)