ОбъяснТак как основание пирамиды ромб, в него можно вписать окружность.
Все двугранные углы при основании равны, значит, высоты боковых граней равны, и их проекции на плоскость основания равны.
Основание высоты пирамиды тогда совпадает с центром вписанной окружности, т.е. точкой пересечения диагоналей.
Площадь полной поверхности пирамиды равна сумме площадей основания и всех четырех боковых граней.
Площадь ромба равна половине произведения его диагоналей.
S ♢=AC*BD:2=48:2=24
Площадь каждой боковой грани равна половине произведения её высоты на основание ( сторону ромба).
Сторону ромба найдем из прямоугольного треугольника АОВ, образованного при пересечении диагоналей.
Его катеты равны половинам диагоналей.
АО=4, ВО=3.
Соотношение катетов 3:4 ⇒ Δ АОВ - египетский и АВ=5
Высоту ромба найдем из его площади.
Площадь параллелограмма ( а ромб - параллелограмм) равна произведению его высоты на сторону, к которой проведена.
Высота ромба равна отношению его площади к стороне. h=24:5=4,8
ОН=h:2=2,4
МН по т. Пифагора равна 2,6 ( проверьте).
S DMC=MH*DC:2=2,6*5:2=6,5
Площадь полной поверхности пирамиды
S=6,5*4+24=50 (ед.площади)ение:
18 см
Объяснение:
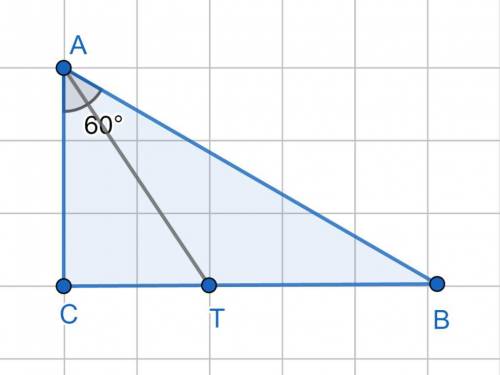
1) Т.к. <C = 90°, <BAC = 60°, то <ABC = 90° - 60° = 30°
2) AT - биссектриса, следовательно по определению она делит угол BAC пополам, а значит <CAT = <BAT = 60° : 2 = 30°.
3)Получаем, что в треугольнике ATB два угла равны 30°, следовательно этот треугольник равнобедренный, т.е. AT = TB = 12 см.
4) Рассмотрим ΔACT: он прямоугольный, <CAT = 30°. Катет лежащий напротив угла 30° равен половине гипотенузы, т.е. CT = AT : 2 = 12 : 2 = 6 (см)
5) CB = CT + TB = 6 + 12 = 18 (см)
ответ: 60 см
Если на РЭШ то пиши без см только 60