
∠BDA = 90° по рисунку.
Потому как BD в данном равнобедренном треугольнике является одновременно биссектрисой, медианой и высотой.
А высота опускается к основанию на 90°.
Объяснение: Через две пересекающиеся прямые AC и BD проведём плоскость АВСD. Четырёхугольник ABCD лежит в одной плоскости, так как две пересекающиеся прямые АС и BD определяют единственную плоскость. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны⇒ АВ ║CD. Тогда треугольникм АКВ и CKD подобны по двум углам (имеем даже три равных угла - <CKD=<AKB как вертикальные, а <BAC(BAK)=<ACD(KCD) и <ABD(ABK)=<BDC(KDC) как накрест лежащие при параллельных AB и CD и секущих АС и BD соответственно). Коэффициент подобия равен k=AB/CD=1/2. Из подобия имеем: KB/KD=1/2 => KD=KB*2 = 10см.
ответ: KD=10см.
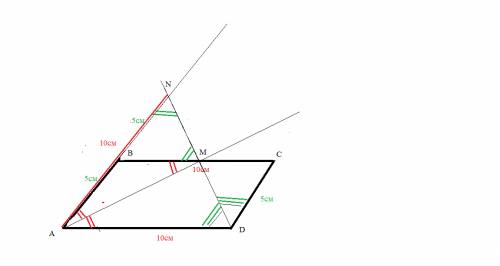
Биссектриса углов А и Д параллелограмма АВСД пересекаются в точке М, дежащий на стороне ВС. Луч ДМ пересекает прямую АВ в точке N. Найдите периметр параллелограмма АВСД, если АN=10 СМ
РЕШЕНИЕ
сделаем построение по условию
<ADN=<CDN т.к. DN - биссектриса <D
(AN) || (CD) тогда <AND=<CDN -скрещивающиеся углы
треугольник NAD - равнобедренный (<AND=<АDN )
|AN|=|AD\=10см
(АМ) - биссектриса, высота, медиана
по теореме Фалеса параллельные прямые (AD) || (BC) отсекают на сторонах <AND
пропорциональные отрезки , т.к. | NM |=| MD | следовательно |NB| = |АB| =|AN| / 2=10/2=5см
ПЕРИМЕТР параллелограмма AB+BC+CD+DA=5+10+5+10=30 см
ответ периметр 30см
90°
Объяснение:
Поскольку треугольник равнобедренный медиана BD, является бисектрисой и высотой. А высота - перпендикуляр, который всегда дает 90°