
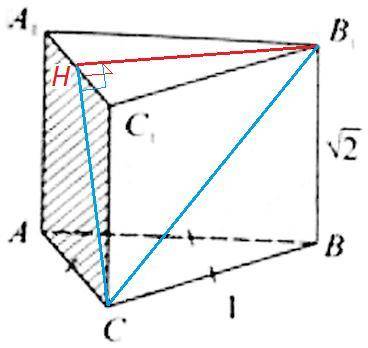
Угол между прямой и плоскостью - угол между наклонной и её проекцией на плоскость.
Чтобы найти проекцию наклонной B1C на плоскость (AA1C) спроецируем точку B1, то есть проведем перпендикуляр B1H к плоскости (AA1C).
Прямая перпендикулярна плоскости если она перпендикулярна двум пересекающимся прямым в плоскости.
Любая прямая в плоскости (A1B1C1) перпендикулярна СС1 (боковые ребра прямой призмы перпендикулярны основаниям). Поэтому достаточно опустить перпендикуляр B1H на A1С1.
B1H⊥A1С1, B1H⊥CC1 => B1H⊥(AA1C)
HC - проекция наклонной B1C на плоскость (AA1C)
B1CH - искомый угол
△B1CH - прямоугольный (B1H⊥HC)
7) B1H =√3/2 (высота в равностороннем △A1B1C1)
B1C =√3 (△B1CB, теорема Пифагора)
sin(B1CH) =B1H/B1C =1/2
B1CH=30
8) HC1 =4 (B1H высота и медиана)
HC =5 (△HCC1 египетский)
cos(B1CH) =HC/B1C =5/10 =1/2
B1CH=60
Площадь осевого сечения цилиндра равна произведению диаметра его основания на высоту.
Поскольку отрезок, соединяющий центр верхнего основания с одним из концов данной хорды образует с осью цилиндра угол 45 градусов, высота цилиндра равна его радиусу r ( см.рисунок).
Площадь осевого сечения даного цилиндра равна
S=r·2r= 2r²
Чтобы найти радиус основания цилиндра, рассмотрим Δ МОВ. Этот треугольник - равносторонний, так как образован хордой и двумя радиусами, угол между которыми равен 60 °.
Высота этог трегольника 2√3, по формуле высоты равностороннего треугольника найдем сторону его а
(а√3):2=2√3, где а=r - сторона треугольника МОВ.
а√3 =2*2√3
а=4
Итак, радиус окружности основания равен 4 см, диаметр 8 см, высота цилиндра 4 см.
S осевого сечения=2r²=32 см²