
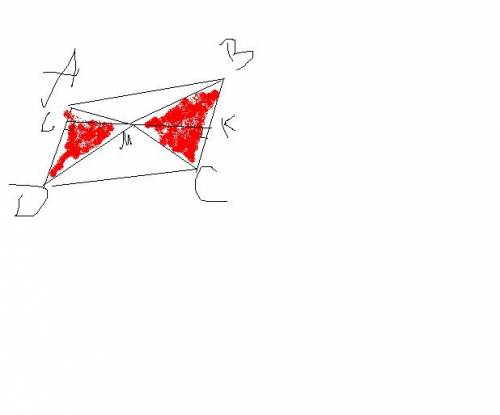
проведем через точку М, пряммую перпендикулярную АD, так как AD||BC, то она будет перпендикулярна и прямой ВС, пусть пряммую AD она пересекает в точке L, а пряммую BC в точке K.
Тогда LM - высота параллелограмма ABCD, LM - высота треугольника ADM, KM - высота треугольника BCM.
Площадь парарлелограмма равна произведению его стороны на высоту, проведенную к этой стороне
Площадь треугольника равна половине произведения стороны на высоту провдеенной к этой стороне
Поэтому
S(AMD)+S(BMC)=1/2*AD*LM+1/2*BC*KM=так противоположные стороны парарлелограмма равны=
=1/2*AD*LM+1/2*AD*KM=1/2*AD*(LM+KM)=1/2*AD*LK=1/2*S(ABCD), что и требовалось доказать
В параллелограмме противоположные углы равны по определению.
Так как противоположные стороны параллелограмма параллельны, то сумма его внутренних односторонних углов, как углов при параллельных прямых и секущей, равна 180º.
∠ВАД+∠СВА=180º
Биссектрисы параллелограмма делят каждый его угол пополам.
Рассмотрим ∆ АВК.
∠ВАК=¹/₂ ∠ВАД
∠КВА=¹/₂∠СВА
¹/₂ ∠ВАД+¹/₂∠СВА =¹/₂ (∠ВАД+∠СВА)=180º:2=90º
Сумма углов треугольника равна 180º,⇒
∠ВКА=в180°-90°=90°
Вертикальный ему угол МКТ четырехугольника КМНТ равен ему и тоже прямой.
Аналогично доказывается, что угол МНТ равен 90º как вертикальный углу СНД,
В ∆ АМД сумма половин внутренних односторонних углов ВАД и СДА равна 90º. ⇒
Угол АМД равен 90º.
Аналогично угол ВТС =90º
Все углы четырехугольника КМНТ, образованного при пересечении биссектрис углов параллелограмма - прямые. ⇒
четырехугольник КМНТ - прямоугольник.