Приведем уравнение заданной прямой к общему виду:
5x + 2y + 4 = 0,
2y = -5x - 4 (делим на 2 обе части уравнения),
у = -2,5x - 2.
Уравнение прямой, параллельной данной, запишем, используя формулу: y - y0 = k(x - x0), где k - угловой коэффициент, x0,y0 - координаты точки, принадлежащей графику, в данном случае точки М. Так как k = -2,5, x0 = 2, y0 = 4, получим:
у – 4 = -2,5 * (х – 2),
у - 4 = -2,5х + 5,
у = -2,5х + 9.
ответ: уравнение параллельной прямой, проходящей через точку М(2; 4), имеет вид у = -2,5х + 9
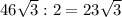 ,
, = 23 * 3 = 69
= 23 * 3 = 69
1)
Дана трапеция ABCD с высотами BO и CK.
Рассмотрим треугольник АОВ-прямоугольный.
Угол ВАО=60 градусов, следовательно, угол АВО=30 гр. Катет, лежащий напротив угла в 30 градусов равен половине гипотенузы, т.е. АО=1/2 АВ, АО=10.
АО=KD=10
AD=32, AD=AO+OK+KD
OK=32-10-10=12
OK=BC
P=AB+BC+CD+AD=20+12+20+32=84
2)
По-моему ОК - эт ополовина SF, поэтому SF=24*2=48