Пусть у треугольника ABC прямой угол А. Значит нам известно отношение сторон AB/BC = 12/13 и AC = 10 см.
Отношение катета и гипотенузы - это синус или косинус какого-либо угла, а именно
sin(C) = 12/13 => C = arcsin(12/13).
cos(B) = 12/13 => B = arccos(12/13).
Формально углы найдены, точное значение предлагаю вычислить самостоятельно, так как я не знаю, в каком виде преподаватель хочет их видеть. К сожалению, из значение является бесконечной десятичной дробью.
Найдем сторону BC.
cos(C) = BC/AC,
BC = cos(C)*AC = 10 * cos(arcsin(12/13)),
Найдем AB.
sin(B) = AC/AB,
AB = AC/sin(B) = 10/sin(arccos(12/13)).
Известно, что arcsin(x) = arccos(sqrt(1-x^2)) при 0 ≤ x ≤ 1 и arccos(x) = arcsin(sqrt(1-x^2)) при аналогичных условиях. Таким образом,
arcsin(12/13) = arccos(sqrt(1-144/169)) = arccos(5/13),
arccos(12/13) = arcsin(sqrt(1-144/169)) = arcsin(5/13).
Отсюда
BC = 10*cos(arccos(5/13)) = 50/13,
AB =10/sin(arcsin(5/13)) = 10/5/13 = 130/5 = 26.
1.
AB=9.6 м
BC=7.2 м
CE =3.6 м - высота к большей стороне
AH - ? - высота к меньшей стороне
S(abc)=1/2*a*h
S(abc)=1/2*AB*CE=1/2*9.6*3.6=17.28 м^2
S(abc)=1/2*BC*AH=1/2*7.2*AH ⇒ AH=S(abc)/3.6=17.28/3.6=4.8 м
высота к меньшей стороне равна 4.8м
2.
AB=BC=12 см
AC = 20 см - основание
S=1/2*a*h
Проведем высоту BH - в равнобед. тр. высота является медианой и биссектрисой ⇒ AH=HC = 1/2*AC = 10 см
По т. Пифагора:
BH=√AB^2-AH^2=√12^2-10^2=√144-100=√44=2√11 см
S(abc)=1/2*20*2√11=10*2√11=20√11 см^2
площадь равнобедренного треугольника равна 20√11 см^2
Объяснение:
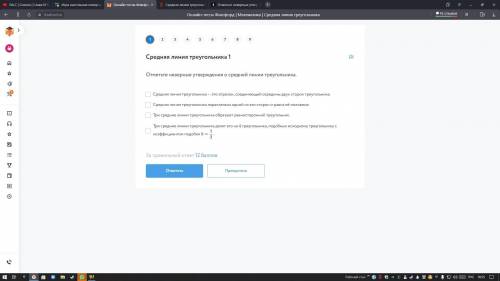
Не верно утверждение №3: Три средние линии треугольника образуют равносторонний треугольник.