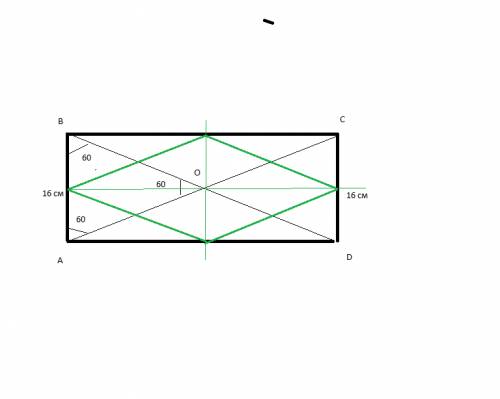
сделаем построение - сразу все видно
точки K L M N - середины сторон прямоугольника АВСД
проведем прямые LN (параллельна АВ и СД) и КМ (параллельна ВС и АД)-
они образуют равные прямоугольники (стороны попарно равны)
KBLO с диагональю KL
OLCM с диагональю LM
NOMD с диагональю NM
АKОN с диагональю KN
и так понятно, что диагонали в равных прямоугольниках равны
KL=LM=NM=KN
но если кто сомневается , то можно доказать через теорему Пифагора
KL^2=KB^2+BL^2
LM^2=LC^2+CM^2
NM^2=MD^2+ND^2
KN^2=AN^2+AK^2
правые части этих выражений равны - это все половинки сторон
а значит равны и левые части
итак все стороны нового четырехугольника равны - это основное свойство РОМБА
если бы начальной фигурой был квадрат - то внутри тоже получился бы квадрат - но у нашего ромба углы 60-120-60-120
Проведем две медианы к боковым сторонам треугольника.
Так как он равнобедренный, медианы эти равны и отсекают от исходного треугольника два меньших, равных между собой.
Угол при основании неизвестен, поэтому обозначим его α и его косинус - cosα
Выразим медиану одного из образовавшихся треугольников по теореме косинусов.
Чтобы найти косинус угла при основании, применим теорему косинусов к данному в условии задачи треугольнику, стороны которого известны.
Подставив найденное значение cosα в уравнение медианы, найдем ее длину.