
РЕШЕНИЕ
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
-боковые ребра правильной пирамиды равны;
-все боковые грани — равные равнобедренные треугольники
высота пирамиды Н=l*sin(b)
основание пирамиды равносторонний треугольник
все углы равны - 60 град
все стороны равны -а
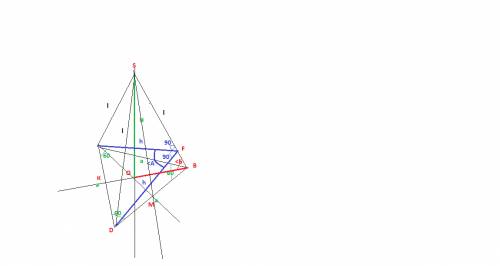
ВК - медиана, биссектриса, высота
ВО=l*cos(b)
BO=2/3*BK
BK=3/2*BO=3/2* l*cos(b)
сторона основания a =BK/sin60=3/2* l*cos(b)/(√3/2)= √3*l*cos(b)
высота боковой грани SM=√(SB^2-MB^2)=√(l^2-(a/2)^2)=√(l^2-((√3*l*cos(b))/2)^2)=
=1/2*l*√(4-3cos^2(b))
выразим ПЛОЩАДЬ треугольника SDB
- через ВЫСОТУ и ОСНОВАНИЕ двумя тогда имеем отношение BD*SM =SB*DF => DF= BD*SM /SB
h=DF=a* 1/2*l*√(4-3cos^2(b)) / l =√3*l*cos(b) *1/2*l*√(4-3cos^2(b)) / l=
=√3/2 *l*cos(b)√(4-3cos^2(b))
теорема косинусов
a^2 = h^2+h^2-2h^2*cosA =2h^2(1-cosA)
cosA=1 - a^2 / (2*h^2)
cosA =1- (√3*l*cos(b))^2 / (2*√3/2 *l*cos(b)√(4-3cos^2(b)))^2 = 1 - 1 / (4-3cos^(b))
A = arccos (1 - 1 / (4-3cos^(b)) )
ответ < A = arccos (1 - 1 / (4-3cos^(b)) ) ; Н=l*sin(b)
ответ: А=С=70г.
В=D=110г.(100г.)
Объяснение: Дано: ABCD - ромб, угол ABO на 20г.(30г.) больше угла BAO.
Найти: углы- А, В, C, D.
Решение: Пусть угол ВАО равен x, по условию угол АВО на 20г.(30г.) больше угла ВАО следовательно угол АВО =x+20. Треугольник АВО - прямоугольный, так как по свойству ромба его диагонали взаимно перпендикулярны, следовательно сумма углов треугольника АВО = 180г. угол АОВ = 90г. Составим уравнение: x+x+20=90
2x=70
x=35
(x+x+30=90; 2x=60; x=30).
угол АВО равен x+20 следовательно угол АВО = 55г. (50г.)
Диагонали ромба являются его биссектрисами (по свойству диагоналей ромба) следовательно угол А = 2ВАО = 70г. угол В = 2АВО =110г.(100г.). По свойству ромба его противоположные углы равны, следовательно угол А = угол С = 70г.
угол В = угол D = 110г.(100г.)