№1 Ну если нарисовать параллелограм в соотношение 3:2, то получиться что на большей стороне по 3 равных отрезка, а на меньшей 2, всего получается 10 частей, а так как периметр равен 30, то надо 30 : 10, получается, что длина отрезка 3 см, а т. к. меньшая часть состоит из двух отрезочков, то 3*2=6
ответ: меньшая сторона 6 см
№2 Я не поняла, но там получается треугольник BNA прямоугольный, но мне кажется что то сдесь не хватает, ну может я чего не знаю.
№3 дана трапеция с основаниями ВС и АД , проведем высоту СН. Рассмотрим четырехугольник ABHD, AD параллельная BH,как перпендикуляры проведенные к одной прямой. AB параллельно DH, как отрезки лежажие на основаниях трапеции., сл-но ABHD параллелограм, поэтому AB=BH=13 см.
Рассм. треугольник BHC- прямоугольный т.к ВН перпендикулярна АВ, сл-но угол АВН =90градусов по скольку Угол АВС 135, то угол НВС=45 градусов. Т.К угол НВС+ угол ВСН=90 градусов, как сумма острых углов в прямоугольном треугольнике, , сл-но угол ВСН = 45градусов, а сл-но треугольник ВСН -равнобедренный с основанием ВС, поэтому ВН=НС=6 см
DC=DH+HC=12 см.
ну и по формуле вычисляешь)
№4 - ...
1)
Не уверена, что правильно поняла термин "неправильные углы". Полагаю, это углы параллелограмма.
Сумма углов при одной стороне параллелограмма равна 180°
В этой сумме 5+7=12 частей.
Одна часть содержит
180:12=15°
Меньший угол
15*5=75°
Больший угол
15*7=105°
---------------------------------------------------------------------------
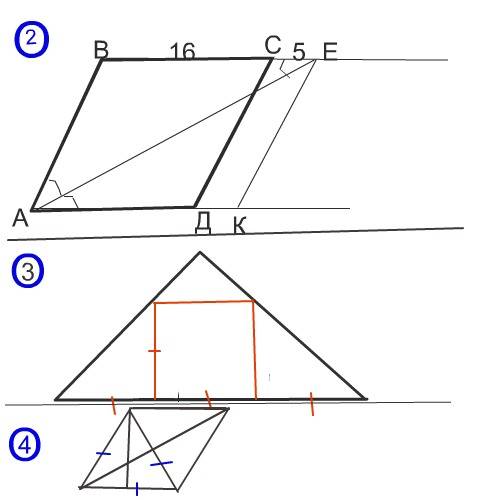
2).
Проведем прямую, параллельную СД из точки Е к продолжению стороны АД. Обозначим точку пересечния К.
Рассмотрим треугольник АВЕ. В нем ∠ ВЕА = ∠ ЕАК , как накрестлежащие при пересечении ВЕ и АК секущей АЕ.
Но по условию задачи∠ ВАЕ равен∠ ЕАК.
Следовательно, треугольник АВЕ - равнобедренный, и АВ=ВЕ.
АВ=16+5=21 см
Периметр АВСД =
2∙(16+21)=74 см
--------------------------------------
3).
Основание вписанного квадрата делит гипотенузу треугольника на три равные части. Отсюда сторона квадрата равна
12:3=4 см
Периметр =4²=16 см ( смотри рисунок)
----------------------
4).
В ромбе высота,проведенная из вершины тупого угла делит его сторону пополам. Половина стороны как катет равна половине стороны, противолежащей прямому углу- гипотенузе.
Отсюда
острый угол ромба равен 60 °, тупой 180-60=°,
а сторона равна меньшей диагонали.
Периметр ромба равен 4*3,5=14 см
Решение*Стороны правильного тетраэдра- правильные трегольники.
*Площадь правильного треугольника S(треуг)=(a^2*sqrt{3}) /4.
*Площадь поверхности правильного тетраэдра
S=4*(a^2*sqrt{3}) /4 = a^2*sqrt{3}.
a^2*sqrt{3}) = 80
a^2=80/sqrt{3}
a=sqrt{80/sqrt{3}} (см)
Ребро второго тетраэдра а1=а/4
Площадь полной поверхности второго тетраэдра равна
S1=(a/4)^2sqrt{3}=(a^2/16)sqrt{3}=(sqrt{80/sqrt{3}})^2 /16 *sqrt{3}=
=80sqrt{3}/(16sqrt{3})=5 (см2)