В равнобедренной трапеции боковые стороны равны,поэтому равны и углы при основаниях.Сумма боковых углов,односторонних равна 180 °,поэтому 268 °-это сумма тупых углов при основании.Сумма всех углов трапеции равна 360°.
Найти меньший угол трапеции можно двумя
1)Из суммы всех углов 360° вычесть суммы тупых углов 268° и разницу разделить на 2 (угла):
°
2)Сумма боковых углов,односторонних равна 180 °,в условии-тупые углы при основаниях и их сумма равна 268°.
Один угол равен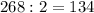 
°.
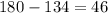°-из суммы боковых углов вычли тупой угол.
ответ:меньший угол трапеции равен 46 °.
33,88
Объяснение:
1) По формуле Герона находим площадь треугольника:
S = √(p · (p-a)·(p-b)·(p-c)),
где p - полупериметр треугольника:
р = P/2 = (17+65+80)/2 = 162:2=81
S = √(81 · (81-17)·(81-65)·(81-80)) = √(81 · 64 · 16 · 1) = √82944 = 288.
2) S = (17·h₁)2 = (65· h₂)/2 = (80· h₃)/2,
где h₁, h₂ и h₃ - высоты, проведённые к соответствующим сторонам треугольника;
следовательно,
2S = 17·h₁ = 65· h₂ = 80· h₃.
Очевидно, что наибольшая высота проведена к наименьшей стороне:
2· 288 = 17·h₁,
откуда h₁ = 576 : 17 ≈ 33,88.
ответ: 33,88.