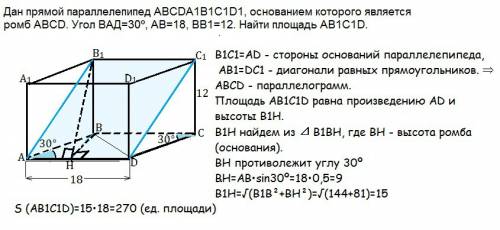
Дан прямой параллелепипед АВСDА1В1С1D1, основанием которого является ромб АВСD. Угол ВАD=30º, АВ=18, ВВ1=12.
Найти площадь AB1C1D.
––––––––––
В прямом параллелепипеде все ребра перпендикулярны основанию, а грани - прямоугольники.
В четырехугольнике AB1C1D стороны В1С1и АD равны как стороны оснований параллелепипеда,
АВ1=DС1 - диагонали равных прямоугольников. ⇒
АВ1С1D - параллело1грамм,т.к. его противоположные стороны равны и параллельны.
Площадь AB1C1D равна произведению АD и высоты, проведенной к АD.
Высота ромба BH - проекция наклонной В1Н на плоскость ромба.
ВН ⊥ АD ⇒
по теореме о 3-х перпендикулярах В1Н⊥ АD и является высотой АВ!С1D
По т.Пифагора из ⊿ В1ВН
B1H=√(B1B²+BH²)
В ромбе высота ВН противолежит углу ВАD=30º
ВН=АВ*sin30º=18*0,5=9
B1H=√(144+81)=15
S (AB1C1D)=15•18=270 (ед. площади)
АВЕ = 104° Следовательно АВС=76 (смежные углы)
, DСF = 76° следовательно АСВ=76 (вертикальные)
САВ- равнобедренный треугольник
АС = АВ= 12 см.
2.В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый
Значит, DМЕ -тупой (смежные углы) и самый большой в треугольнике ЕМD. Против большего угла лежит большая сторона. Следовательно, DE>DM. Что и требовалось доказать
Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.
а-сторона, а+9 - основание треугольника
а+а+а+9=45
3а= 36
Стороны треугольника равны: а=12 а+9=21
12+12+21= 45
Радиус, проведённый в точку касания перпендикулярен касательной. Значит АО перпен-но АВ, и треугольник АОВ прямоугольный. Угол ВАО=90 град. АО=R=AB*tg30=6√3*√3/3=6