ответ: Объем шарового сегмента опущенного в цилиндр = π*468 см³
Объяснение: Дано:
Диаметр шара = 30 см тогда его радиус R = 15
Радиус основания цилиндра r = 12см
Найти объем шарового сегмента, опушенного в цилиндр V - ?
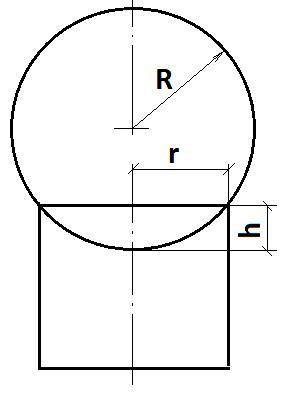
Смотрите рисунок. Что бы найти объем надо найти размер h - глубину погружения шара. По теореме Пифагора R² = r² + (R-h)² Получили квадратное уравнение: h² - 2Rh + r² = 0
h1,2 = (2R+-√4R² - 4r²)/2 = (2R+-2√R²-r²)/2 h = 6 см
Объем шарового сегмента найдем по формуле V = π*h²(R - h/3) = π*468 см³
1) AB = 15
2) AB = 20
Объяснение:
Первый случай, кода AB не пересекает плоскость.
Тогда получаем прямоугольную nрапецию ABB'A'. О - точка пересечения высоты, опущенной из точки A на сторону BB'.
Получаем прямоугольный треугольник ABO
OB=BB'-AA' = 12.5-3.5 = 9
AO = A'B' = 12
По теореме Пифагора получаем
Второй случай, когда AB пересекает плоскость.
Тогда получаем фигуру из двух подобных треугольников (подобие по двум углам, один прямой, второй накрест лежащий, но этот факт нам не понадобится).
Достроим прямоугольный треугольник с прямым углом С продлив сторону AA' восстановив перпендикуляр к этой стороне из точки B.
Получаем прямоугольный треугольник ABC, при этом
AC = AA' + BB' = 12.5+3.5=16
BC = A'B = 12
По теореме Пифагора получаем