Объяснение:
Дано:
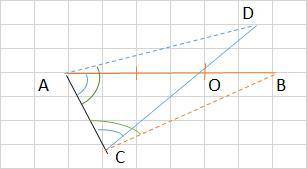
АВ = СD
АО : ОВ = СО : OD = 2 : 1
Док., что ΔАСD = ΔСАВ
Т.к. АВ = СD, то АО = СО и ОВ = OD
Пусть ОВ = ОD = х, тогда
АО = СО = 2х
1) ΔАОС - равнобедренный, т.к. АО = ОС, следовательно,
∠ОАС =∠ОСА
2) Рассмотрим ΔАСD и ΔСАВ
АВ = СD по условию,
∠ВАС (ОАС) = ∠DСА (ОСА)
АС - общая сторона. Значит,
ΔАСD = ΔСАВ по 1 признаку (по 2-м сторонам и углу между ними), ч.т.д.
б) Т.к. ΔАСD = ΔСАВ, то
∠DAC = ∠ ВСА или
∠ОАD + ∠САВ = ∠ОСВ + ∠DСА
Но ∠САВ = ∠DСА, значит, и
∠ОАD = ∠ОСВ = 50°
3.
В прямоугольном треугольнике высота, проведенная к гипотенузе, может быть вычислена через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:
h = √ху = 12
12² = ху
ху = 144
Если гипотенуза ВС = 20 см, то
у = 20 - х, подставляя в уравнение, получим:
х( 20 - х) = 144
х² - 20х + 144 = 0
D = (-20)² - 4*1*144 = 400 - 576 = - 176
D < 0 - т.к. дискриминант меньше нуля, то у квадратного уравнения корней нет.
Следовательно, гипотенуза не может быть равна 20ед.
Даны уравнения высоты CD: 3x + 4y − 15=0, биссектрисы BL: 3x − y − 4 = 0 и координаты вершины A (4; 3) треугольника АВС.
Находим уравнение стороны АВ как перпендикуляра к высоте CD (используя свойство перпендикулярной прямой: коэффициенты А и В меняются на В и (-А)).
AB: 4x - 3y + C = 0, подставляем координаты точки А.
4*4 - 3*3 + С = 0, отсюда С = 9 - 16 = -7.
Уравнение АВ: 4х - 3у - 7 = 0.
Находим координаты точки В как точки пересечения АВ и BL.
4x - 3y - 7 = 0, 4x - 3y - 7 = 0
3x - y - 4 = 0 умн.на-3 = -9x + 3y + 12 = 0
-5x + 5 = 0, x = 5/5 = 1.
y = 3x - 4 = 3*1 - 4 = -1.
Точка В(1; -1).
Переходим к стороне ВС как симметричной АВ относительно BL.
Угловые коэффициенты прямых:
k1(AB) = (4/3), k2(BL) = 3.
Тангенс угла между ними (разность угловых коэффициентов) опредляем по формуле:
k = (k2 - k1) / (1 + k2*k1) = (3 - (4/3)) / (1 + 3*(4/3)) = 1/3.
Находим k(BC) = (3 + (1/3)) / (1 - 3*(1/3)) = ∞.
То есть, ВС - это вертикальная линия с уравнением х = 1.
Уравнение ВС: х = 1.
Определяем координаты точки С при х = 1.
у(С) = (15 - 3*1) / 4 = 3. Точка С(1; 3).
Так как по оси Оу координата совпадает, то это - горизонтальная линия с у = 3.
Уравнение АС: у = 3.