основание-14 см, боковая сторона-21 см
Объяснение: основание-2х
боковые стороны-3х
Р-56 см
уравнение: 3х+3х+2х=56
8х=56
х=7 см
основание: 2*7=14 см
боковая сторона: 3*7=21
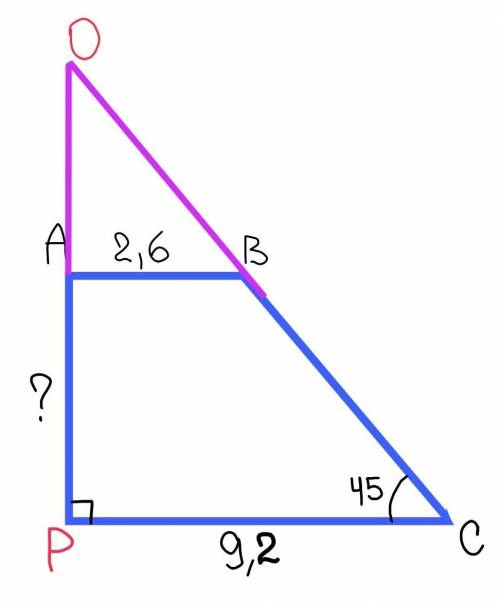
Продлим РА за точку А и СВ за точку В, точку пересечения назовём О.
∆РОС – прямоугольный с прямым углом Р.
Сумма острых углов прямоугольного треугольника равна 90°. Исходя из этого: угол РОС=90°–угол ОСР=90°–45°=45°.
Получим что угол РОС=угол ОСР, тогда ∆РОС – равнобедренный с основанием ОВ.
Тогда РО=РС=9,2 см.
Основания трапеции параллельны, тоесть АВ//РС.
Следовательно: угол ОВА=угол ОСР как соответственные при параллельных прямых АВ и РС и секущей ОС; тогда угол ОВА=45°.
Угол АОВ=45° (доказано ранее)
Получим что угол ОВА=угол АОВ.
Тогда ∆АОВ – равнобедренный с основанием ОВ. Следовательно АО=АВ=2,6 см.
РА=РО–АО=9,2–2,6=6,6 см.
ответ: 6,6 см.
Проводим линию параллельную меньшей боковой стороне трапеции от угла, который между меньшим основанием и большей боковой стороной трапеции. Мы получаем прямоугольный треугольник, два угла которого равны 45 и 90 градусам.
Следующий шаг - отнимаем от большего основания меньшее - 10,7-2=8,7 (см) - длина большего основания за линией или один из катетов угла.
Так как сумма углов треугольника равна 180 градусам, то находим оставшийся угол этого самого треугольника - 180-90-45=45 градусов.
Угол в 45 градусов равен второму углу в 45 градусом, следовательно, этот треугольник - равнобедренный и его второй катет равен 8,7 см.
Так как второй катет проведен параллельно меньшей боковой стороне, то они, соответственно, равны 8,7 см.
ответ 8,7 см
В равнобедренном треугольнике боковые стороны равны, тогда составляем уравнение.
2x - основание, тогда 3x - боковая сторона (всего их две).
2x + 3x + 3x = 56
8x = 56
x = 56/8 = 7
7*2 = 14 см (основание).
7*3 = 21 см (боковая сторона).
ответ: 14 см.