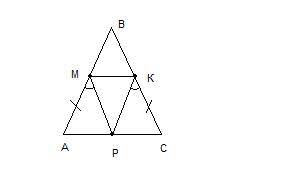
1)АВС - равнобедренный, тогда уголА=углуС(при основании), также
угол AMP=углу PKC и AM=KC(по условию),
то треугольникAMP=треугольникуPKC (по стороне и 2ум прилежащим углам), значит
все элементы в них равны, тогда АР=РС, значит ВР-медиана,
а в равнобедренном треугольнике медиана, проведенная из угла между боковыми сторонами является ещё и высотой и биссектрисой.
2)АМ=КС(по условию), причем уголА=углуС(при основании), значит
АМКС - равнобедренная трапеция, тогда МК параллельно АС.
т.к.ВР и медиана и биссектриса и высота [см. 1) доказательство],
то ВР перпендикулярно АС, но т.к. МК параллельно АС, то
ВР перпендикулярно МК
Надеюсь удачи ! )
PE =√(ME^2 -PM^2) =9 (т Пифагора)
MH =PK (противоположные стороны прямоугольника) =PE+EK =9+6 =15
S(MEKH) =1/2 (EK+MH)PM (площадь трапеции) =1/2 (6+15)12 =126 (см^2)