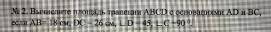
1) Периметр трапеции ABCD равен 72 см.
2) Углы четырехугольника, вписанного в окружность:
∠A = 10°; ∠B = 165°; ∠C = 170°; ∠D = 15°.
3)Градусная мера дуги, которую отсекает от окружности большее основание трапеции, равна 305°.
Объяснение:
1) Требуется найти периметр прямоугольной трапеции, в которую вписали окружность.
Дано: АВСД - прямоугольная трапеция.
Окр.О,R;
∠D=30°;
ОМ = 6 см.
Найти: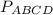 
.
Для того, чтобы найти периметр, необходимо найти все стороны трапеции.
1. Рассмотрим АВРК.
Радиус, проведенный в точку касания, перпендикулярен касательной.⇒ АВРК - прямоугольник.
AB = 2R = 6*2 = 12 (см)
Противоположные стороны прямоугольника равны.ВР = АК = R = 6 см
2. Рассмотрим ΔНСD - прямоугольный (СН - высота).
∠D = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ CD = 2*CH = 12 * 2 = 24 (см)
3. CD = CE + ED = 24 см.
Отрезки касательных к окружности, проведенные из одной точки, равны.⇒ PC = CE; KD = DE.
или РС + KD = 24 см.
4. Теперь найдем периметр трапеции ABCD.
Периметр - сумма длин всех сторон.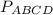 = AB + BC + CD + AD = AB +BP + PC + CD + AK + KD =
= 12 + 6 + 24 +24 + 6 = 72 (см)
Периметр трапеции ABCD равен 72 см.
2) Требуется найди все углы четырехугольника, вписанного в окружность.
Дано: ABCD - вписанный четырехугольник.
∠C + ∠D = 185°; ∠C - ∠D = 155°
Найти: ∠A; ∠B; ∠C; ∠D.
Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна 180°.Так нам дана сумма углов, равная 185°, то рассматривать противоположные углы мы не можем. Поэтому выбрали ∠С и ∠D.
1. По условию
∠C + ∠D = 185°
∠C - ∠D = 155°
Сложив эти два уравнения, получим:
2∠С = 340° |:2
∠C = 170°
Подставив это значение в любое из уравнений, получим
∠D = 15°
2. Теперь найдем остальные углы четырехугольника, вписанного в окружность.
∠A + ∠C = 180° ⇒ ∠A = 180° - 170° = 10°
∠B + ∠D = 180° ⇒ ∠B = 180° - 15° = 165°
Углы четырехугольника, вписанного в окружность:
∠A = 10°; ∠B = 165°; ∠C = 170°; ∠D = 15°.
3) Требуется найди градусную меру дуги, которую отсекает от окружности большее основание трапеции.
Дано: Окр.О;
ABCD - трапеция, вписанная в окружность.
∪АВ = 20°; ∪ВС = 15°
Найти: ∪АmD.
Если трапецию можно вписать в окружность, то трапеция – равнобедренная.⇒ ABCD - равнобедренная трапеция, то есть
AB = CD.
Равные хорды стягивают равные дуги.⇒ ∪АВ = ∪CD = 20°
Градусная мера всей окружности равна 360 °.⇒ ∪АmD = 360° - (∪АВ + ∪ВС +∪CD) = 360° - 55° = 305°
Градусная мера дуги, которую отсекает от окружности большее основание трапеции, равна 305°.
АВ: y = 2x + 1
ВС: y = -0,5x + 3,5
АС: y = 1/3x – 2/3
Рівняння кола (х²-2)+у²= 3,2²
Объяснение:
АВ
формулой канонического уравнения прямой:
(x - xa)/(xb - xa )= (y - ya)/(yb - ya)
Подставим в формулу координаты точек:
(x - (-1))/(1 - (-1)) = (y - (-1) /(3 - (-1))
В итоге получено каноническое уравнение прямой:
x + 12 = y + 14
Из уравнения прямой в каноническом виде получим уравнение прямой с угловым коэффициентом:
y = 2x + 1
ВС – уравнение прямой y = -0,5x + 3,5
АС
формулой канонического уравнения прямой:
(x - xa)/(xb - xa )=( y - ya)/(yb - ya)
Подставим в формулу координаты точек:
(x - (-1))/(5 - (-1) ) = (y - (-1) ) /(1 - (-1) )
В итоге получено каноническое уравнение прямой:
x + 16 = y + 12
Из уравнения прямой в каноническом виде получим уравнение прямой с угловым коэффициентом:
y = 1/3x – 2/3
Формула окружности с центром (a;b) и радиусом R имеет вид
(х²-х₀)+(у²+у₀)= r²
или если мы раскроем скобки
х²+у²-2х₀х-2у₀у-(r²-х₀²-у₀²)=0
после подставки координат точек
Получена формула окружности
х²+у²-4х-6=0
Центр окружности х₀= –а₄/2а₁, у₀= -а₅/2а₁,
а₄=-4; а₁=1; а₅=0;
х₀= –а₄/2а₁=-(-4)/(2*1)=2
у₀= -а₅/2а₁=0/(2*1)=0
а₆=-6
Радиус окружности
r= ((а₄/2)²+ (а₅/2)²- а₁а₆)/ |а₁|
r=((-4/2) 2+0-1*(-6)/1=3,2
(х²-2)+у²= 3,2²