
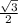 a ⇒
a ⇒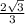 h
h 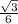 a =
a =  h
h 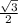 a ⇒
a ⇒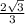 h =
h = 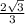 m =
m = 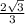 l
l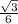 a =
a =  h =
h =  m =
m =  l
l h = 10 см
h = 10 см h = 1,4 (м)
h = 1,4 (м) h = 1
h = 1 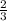 (см)
(см) h = 1,2 (см)
h = 1,2 (см) h = 3,7 (см)
h = 3,7 (см) m = 7 (см)
m = 7 (см)  m = 0,3 (мм)
m = 0,3 (мм)  m = 2
m = 2 (дм)
(дм)  m = 1,8 (см)
m = 1,8 (см)  m = 12,4 (см)
m = 12,4 (см)  l = 18 (мм)
l = 18 (мм)  l = 2
l = 2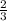 (м)
(м)  l = 24 (см)
l = 24 (см) l = 3,2 (см)
l = 3,2 (см)
Опустим перпендикуляр АМ на основание (он будет и медианой стороны а и биссектрисой угла А).
Из середины стороны в восстановим перпендикуляр до пересечения с высотой АМ в точке О - это центр описанной окружности. Из точки О опустим перпендикуляр ОК на сторону в. В полученном треугольнике ОКС угол КОС равен углу В (как половина центрального угла, равного вписанному углу 2В).
По теореме косинусов cos B = (b²+a²-b²) / 2ab = a / 2b.
sin B = √(1-cos²B) = √(1-( a / 2b.)²) = √(1-a²/4b²).
Из треугольника ОКС (где ОС=R) находим b/2R = sin B.
Тогда R = b² / √(4b²-a²).
Для определения радиуса вписанной окружности из вершины С проведем биссектрису СО₂. Точка О₂ - центр вписанной окружности.
r = (a/2)*tg (C/2).
Используя формулу tg(C/2) = +-√((1-cos C) / (1 + cos C)), находим:
r = (a/2)*√((2b-a) / (2b+a)).