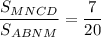
Объяснение:
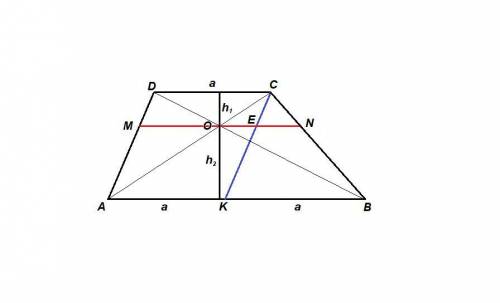
CD = a, AB = 2a.
ΔAOB ~ ΔCOD по двум углам (∠ОАВ = ∠ОСD как накрест лежащие при пересечении AB║CD секущей АС, углы при вершине О равны, как вертикальные)
Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно отношению сходственных сторон, т.е.
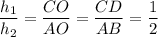
h₁ / h₂ = 1/2 ⇒ h₂ = 2h₁
______________________________________
MN║AB║CD, тогда по обобщенной теореме Фалеса
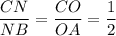
Проведем СК║AD. СК∩MN = E.
ADCK - параллелограмм, значит АК = CD = a.
KB = AB - AK = a
MDCE параллелограмм (MD║CE и ME║CD ), значит ME = CD = a.
ΔCEN ~ ΔCKB по двум углам (∠CEN = ∠CKB как соответственные при пересечении EN║KB секущей СК, угол С общий)
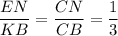
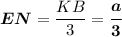
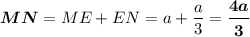
______________________
Площадь верхней трапеции:
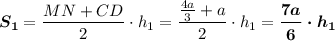
Площадь нижней трапеции:
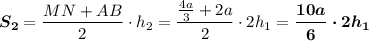

1.
наименьший угол - тот который лежит против меньшей стороны (9 см)
sin(a) = 9/41
cos(a) = 40/41
tg(a) = 9/40
ctg(a) = 40/9
2.
кос=катет:гипотенуза
отсюда следует что катет=косинус*гипотенузу=20*0,8=16(см)
по теореме Пифагора находим другой катет:
катет(второй) в кв=гипотенуза в кв - катет(первый)в кв=20 в кв - 16 в кв=400-256=144
катет(второй)=12(см)
3.
tg(a) = 2.5 / 2.5√(3) = 1 / √(3)
a = arctg(a) = arctg(1 / √(3)) = 30°
tg(B) = 2.5√(3) / 2.5 = √(3)
B = arctg(B) = arctg(√(3)) = 60°