
Высота этого треугольника, опущенная на гипотенузу из вершины прямого угла, равна 9:6·2= 3 см
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Найдем эти отрезки, обозначив один из них х, другой 6-х:
9=х(6-х)
9=6х-х²
3²= x *(6-x)
х²-6х+9=0
Решив это квадратное уравнение, найдем два одинаковых корня х=3
Следовательно, отрезки, на которые высота делит гипотенузу, равны, и треугольник - равнобедренный.
Высота равна 3, половина гипотенузы=3.
Из прямоугольного треугольника с катетами 3 и 3 найдем боковую сторону ( катет исходного треугольника)
х²=3²+3²=18
х= √18=3√2
Катеты равны 3√2
Проверка:
Площадь найдем половиной произведения катетов:
S= (3√2)·(3√2):2=9·2:2=9 cм²
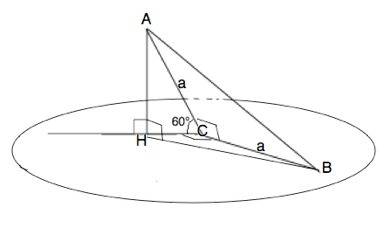
Через катет прямоугольного равнобедренного треугольника проведена плоскость, которая образует с плоскостью треугольника угол 60°. Найдите углы, которые образуют 2 другие стороны треугольника с этой плоскостью.
Обозначим треугольник АВС. АС=ВС, угол С=90°
Проведенная плоскость и плоскость треугольника образуют двугранный угол, линейным углом которого являются два перпендикуляра к его ребру в точке С.
Угол АСВ - прямой, ⇒АС- перпендикуляр в плоскости треугольника к линии пересечения плоскостей, НС - перпендикуляр, проведенный в проведенной плоскости к той же линии.
Угол АСН =60°
АН - перпендикуляр к плоскости, НВ - проекция гипотенузы АВ на плоскость.
Угол АВН - искомый.
В равнобедренном прямоугольном треугольнике острые углы равны 45°.
Примем катеты ∆ АВС равными а. Тогда гипотенуза
АВ=а:sin 45°=a√2
АН=а•sin60°=a√3/2
sinАВН=АН:АВ=a√3/2):a√2=0,61237
Это синус угла ≈37,76°
Объяснение:
Мне кажется, тут нужно применить теорему Пифагора, но я пока не понимаю, как