М∈АВ
N∈BC
P∈AC
И делит стороны так, что
MB=2AM, NC=2BN, AP=2PC, т.е. соотношение1:2
Отношение площадей треугольников имеющих равный (общий) угол равно произведению сторон содержащих этот угол. Доказательство этого факта приводить не буду. Желающие найдут (сделают :-) сами.
Рассмотрим, исходя из этого, треугольники АВС и AMP.
S(ABC)/S(AMP) = (AB*AC)/(AM*AP) (1)
Примем меньший отрезок АМ за 1 часть, соответственно MB будет 2 части.
Т.е. AB/AM = 3/1, AC/AP=3/2, подставим эти соотношения в выражение (1) для соотношения площадей треугольников получим:
S(ABC)/S(AMP) = (3*3)/(1*2) = 9/2, т.е. S(AMP)=(2/9)*S(ABC) =(2/9)*S
Можно провести аналогичные рассуждения для оставшихся треугольников, но учитывая соотношения сторон легко :-) заметить, что площади всех маленьких треугольников AMP, MBN, PNC равны и равны (2/9)*S.
Т.о. искомая площадь треугольника MNP будет равна
S-3*((2/9)*S) = 1/3 S, одной трети площади ABC, равной S.
И ещё. В чем смысл подобных задач? В том что ты учишься находить решение.
Сегодня это геометрия. Через годы это будут другие, более серьезные проблемы. На этом сайте ты научишься только списывать. Скачай себе
"Гордин-Планиметрия 7-9" и реши хотя бы одну задачу на соотношение площадей. Тогда я буду считать, что не зря потратил время, набивая всё это.
С тебя "69" :-)
Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
По т. Пифагора а²+b²=(3+4)² ,(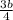 )²+b²=49 ,
)²+b²=49 ,
a=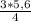 =4,2 cм
=4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."