Треугольник ABC в гомотетии отображается в треугольнике A1B1C1 AB-7, BC-18,AC-23 найдите длину короткой стороны треугольника A1B1C1 если длина длиной стороны этого треугольника равна 115
Значит сначала мы должны найти площадь основания пирамиды, а затем площадь боковой поверхности пирамиды.
В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому (см²).
Площадь боковой поверхности правильной четырёхугольной пирамиды - полупроизведение периметра основания на апофему.
Значит нам нужно сначала найти апофему нашей пирамиды.
1 правило: Апофема делит сторону основания пополам.2 правило: Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.
Объяснение 1 правила: из этого следует, что апофема делит сторону основания так, что (см).
Объяснение 2 правила: внутри нашей пирамиды образовался прямоугольный , где - катет прямоугольного тр-ка (высота пирамиды); - катет прямоугольного тр-ка; - гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что (см).
Так как апофема нашей пирамиды является ещё и гипотенузой прямоугольного , то мы сможем найти её величину по т.Пифагора:
(см).
Теперь найдём периметр основания (квадрата):
(см).
Затем найдём площадь боковой поверхности:
(см²).
Остаётся найти ответ на вопрос: "Чему равна площадь полной поверхности пирамиды?"
Однажды под Рождество, произошло настоящее волшебство, но только в реальной жизни. Девочка Маша с самого рождения жила в детском доме. У неё никогда не было красивых платьев, игрушек. Но ей этого не сильно и хотелось. Каждый год, в течение 10 лет она загадывала одно и тоже желание. Ей хотелось обрести семью. Ей хотелось чтобы у неё была мама и был папа.И вот наконец, случилось чудо под Рождество. За Машей пришли родители, которые забрали её в новый, красивый, тёплый дом. Где они стали втроём жить. Мама,папа и Маша. И с этого момента у них началась настоящая счастливая жизнь.
Правильная четырёхугольная пирамида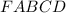
.
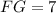(см).
Найти: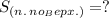
(см²).
Решение:Значит сначала мы должны найти площадь основания пирамиды, а затем площадь боковой поверхности пирамиды.
В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому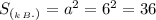
(см²).
Площадь боковой поверхности правильной четырёхугольной пирамиды - полупроизведение периметра основания на апофему.
Значит нам нужно сначала найти апофему нашей пирамиды.
1 правило: Апофема делит сторону основания пополам.2 правило: Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырехугольной пирамиды.Объяснение 1 правила: из этого следует, что апофема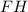
делит сторону основания 
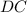так, что 
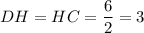(см).
Объяснение 2 правила: внутри нашей пирамиды образовался прямоугольный
, где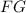 
- катет прямоугольного тр-ка (высота пирамиды); 
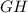- катет прямоугольного тр-ка; 
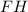- гипотенуза прямоугольного тр-ка (апофема пирамиды). По данному правилу можно сказать, что 
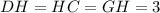(см).
Так как апофема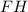
нашей пирамиды является ещё и гипотенузой прямоугольного 
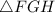, то мы сможем найти её величину по т.Пифагора:
Теперь найдём периметр основания (квадрата):
Затем найдём площадь боковой поверхности:
Остаётся найти ответ на вопрос: "Чему равна площадь полной поверхности пирамиды?"
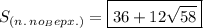(см²).
ответ: