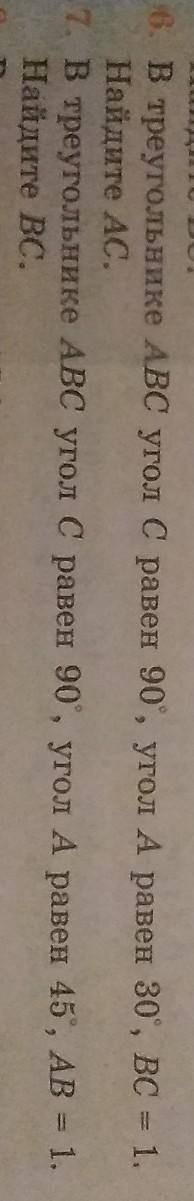
Рисунок - во вложении.
Т.к. E и F - внутренние точки отрезка АВ, и по условию АЕ=BF, то
для EB=AB-AE и для AF=AB-BF следует, что EB=AF.
Рассмотрим прямоугольные ΔADF и ΔВСЕ. У них: 1) АD=BC (противолежащие стороны прямоугольника); 2) AF=EB (по доказанному выше). Значит, ΔADF = ΔВСЕ по двум катетам.
Из равенства этих треугольников следует, что ∠DFA=∠СЕВ. Отсюда, ΔEGF - равнобедренный с основанием EF, тогда GF=GE. Доказан пункт Б).
Т.к. АВСD - прямоугольник, то АВ║CD. Тогда ∠EFG=∠GDC(как накрестлежащие при секущей FD) и ∠FEG=∠GCD (как накрестлежащие при секущей ЕС). Отсюда, ΔDGС - равнобедренный с основанием DC, тогда DG=GC. Доказан пункт A).

Задача 6
Т. к. угол С=90, угол А=30, уголВ=180-90-30=60 ⇒ катет, лежащий против угла в 30 градусов равен половине гипотенузы.
АС=2*ВС=2*1=2
Объяснение:
Задача 7. ∠С = 90°, угол А = 45 по условию, ∠В = 90° - 45° = 45°. Тогда ∠В = ∠А => ∆ABC - равнобедренный.
АВ=1 основание треугольника, АС=ВС= 1/2АВ = 0,5