1) Все грани куба равны. Площадь диагонального сечения куба равна произведению длины ребра куба на длину диагонали грани.
S=a•d
Диагональ грани куба делит её на равнобедренные треугольники с острым углом 45°.
d=a:sin45°=a√2
S=a•a√2=a²√2
У куба 6 граней. Площадь одной грани
а²=18√2:6=3√2
S=3√2•√2=6 см²
------------
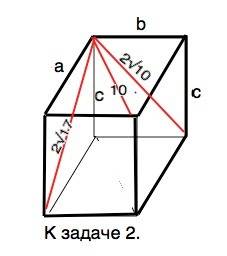
2) Сделаем рисунок. Примем длины ребер, исходящих из одной вершины, равными a, b, c.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений:
D²=a²+b²+c²
Квадраты диагоналей граней равны:
a²+b²=10²=100
a²+c*=(2√17)²=68
b²+c²=(2√10)²=40 , откуда
2•(a²+b²+c²)=208
D²=208:2=104 ⇒
D=√104=2√26 см
-------
3) Боковые грани прямой призмы - прямоугольники. Т.к. в основании данной призмы ромб, то одна сторона грани - сторона ромба, другая - высота призмы.
В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон. Ромб - параллелограмм, все стороны которого равны. Примем сторону ромба равной а. Тогда
4а²=8²+6²=100⇒
а²=25, а=5 см
Диагональ прямоугольника со сторонами 12 см и 5 см равна 13 см ( отношение сторон из Пифагоровых троек). Можно по т.Пифагора найти с тем же результатом.
Доказываем равенство треугольников по свойству касательных из одной точки,
Тогда угол KON=MOK и они по 60 градусов. 120/2=60 градусов.
Есть два прямоугольных треугольника. Радиусы ON и OM находятся по свойство угла в 30 градусов, т.е.
2ON=OK
2ON=12 /2(ДЕЛИЛИ ОБЕ ЧАСТИ)
ON=6
Затем находим всё по теореме Пифагора.
KN+ON=OK(все величины в квадрате)
KN2+36=144
KN2=144-36=108 градусов.
корень из KN=корень из 108 радусов и это 6 корней из 3.
KN=KM(по свойству отрезков касательных)
ответ:KN=KM=6 корней из 3.
отрезки касательных, проведённых из одной точки к окружности равны и образуют равные углы с прямой, проходящей через центр окружности и точку, из которой проведены касательные, поэтому МК=КN, угол ОКN=углу ОКМ, угол ОМК=углу ОNК=90 градусов по свойству касательных, тогда угол КОТ= углу КОМ=120:2=60 градусов. По соотношениям в прямоугольном треугольнике КМ=ОК*sin60=12*√3/2=6√3