ба треугольника прямоугольные, значит, C = C1 = 90°.
Кроме того, острые углы A = A1 по условию.
Значит, B = B1 = 90° - A - третьи углы тоже равны.
Если равны хотя бы одна пара сторон (например, AB = A1B1), то эти треугольники будут равны.
Если ни одна сторона одного треугольника не равна соответствующей стороне другого треугольника, то эти треугольники подобны.
Объяснение:
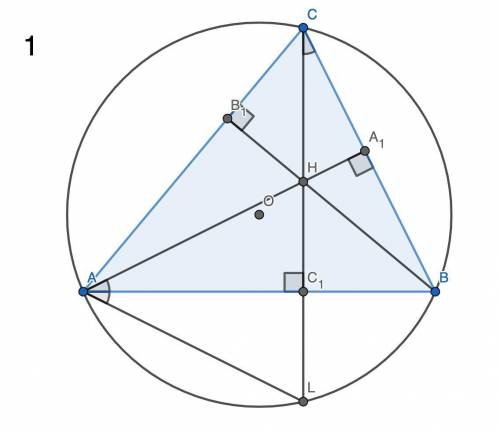
1) В треугольниках ΔAA₁B и ΔСС₁B углы ∠A₁ и ∠C₁ — прямые, угол ∠B — общий. Значит, углы ∠A₁AB и ∠С₁CB (∠LCB) равны (так как все углы каждого треугольника должны в сумме давать 180°).
Углы ∠LAB и ∠LCB опираются на одну дугу, значит, они равны.
∠A₁AB = ∠LCB, ∠LCB = ∠LAB ⇒ ∠A₁AB = ∠LAB. Тогда прямоугольные треугольники ΔAC₁H и ΔAC₁L равны по общему катету AC₁ и прилежащему к нему углу (∠A₁AB = ∠LAB). Значит, их соответствующие элементы равны, в частности, HC₁ = C₁L, что и требовалось доказать.
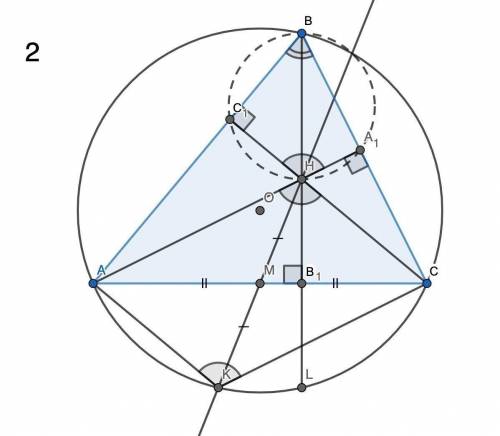
2) AM = MC, HM = MK по условию ⇒ AKCH — параллелограмм ⇒ ∠AKC = ∠AHC. ∠AHC = ∠A₁HC₁ как вертикальные ⇒ ∠AKC = ∠A₁HC₁.
∠BA₁H = ∠BC₁H = 90° (в сумме дают 180°) и опираются на один отрезок (лежат по разные стороны этого отрезка). Значит, около четырёхугольника A₁BC₁H можно описать окружность. Но тогда ∠A₁HC₁ = 180° - ∠A₁BC₁. А поскольку ∠AKC = ∠A₁HC₁, то ∠AKC = 180° - ∠A₁BC₁. Значит, четырёхугольник ABCK — вписанный, K лежит на описанной около ABC окружности, что и требовалось доказать.
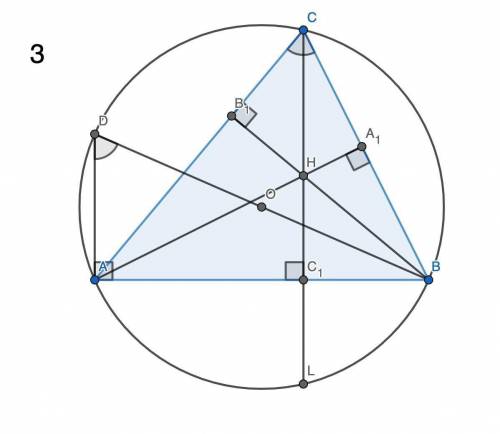
3) Продлим BO до пересечения с окружностью в точке D — получим диаметр BD. Тогда ∠BAD — прямой, так как опирается на диаметр. В треугольниках ΔBAD и ΔBB₁C: ∠BAD = ∠BB₁C = 90°, ∠ADB = ∠ACB как опирающиеся на одну дугу. Значит, углы ∠ABD и ∠CB₁B также равны. Но это те же углы, что и ∠ABO и ∠CBH соответственно. Значит, ∠ABO = ∠CBH, что и требовалось доказать.
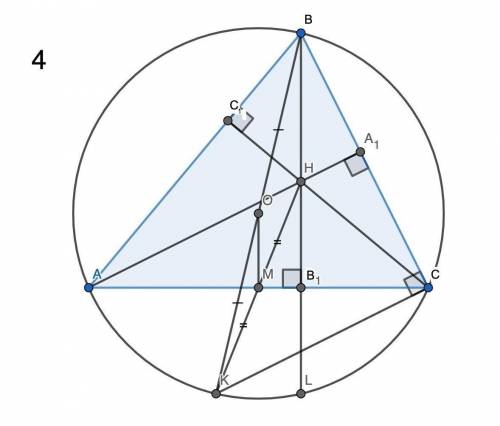
4) Пусть HM = MK. Тогда K лежит на описанной окружности по п. 2. Также по п. 2 AKCH — параллелограмм ⇒ AH║KC, но AH⊥BC ⇒ KC⊥BC. ∠KCB — прямой, значит, KB — диаметр ⇒ KO = OB.
Рассмотрим ΔKOM и ΔKBH: ∠K — общий, KO : KB = 1 : 2, KM : KH = 1 : 2 по построению ⇒ треугольники подобны ⇒ OM : BH = 1 : 2 ⇒ BH = 2OM, что и требовалось доказать.
Если катет и прилежащий острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему углу другого прямоугольного треугольника, то эти треугольники равны. Значит надо проверить равенство прилежащего катета ответ ВОбъяснение: