Варiант 2 Початковий та середній рівні навчальних досягнень
У завданнях 1-6 виберіть правильну відповідь.
1. За якими елементами можна встановити рівність трикутників?
А) За двома сторонами і яким-небудь кутом;
Б) за трьома кутами; В) за стороною і якими-небудь двома кутами;
Г) за трьома сторонами.
2. Визначте за рисунком, яка
з наведених рівностей неправильна.
70
A) АВ = 7; Б) BDC = 70°;
D
В) ДАВD = ДСDB; Г) ZBCD = 70°.
3. Як називається перпендикуляр, проведений із вершини трикут-
ника до прямої, що містить протилежну сторону?
А) Бісектриса; Б) основа; В) висота; Г) медіана.
4. У трикутнику ABC ZA = 20. Які сторони цього трикутника рівні?
A) AB = BC; Б) AC = AB; В) АС = ВС; Г) АВ = ВС = АС.
5. Периметр рівнобедреного трикутника дорівнює 20 см, а його
бічна сторона — 7 см. Знайдіть основу трикутника.
А) 6,5 см; Б) 12 см; В) 6 см; Г) 8 см.
6. MN бісектриса рівнобедреного трикутника KMP. За якої
з наведених умов AKMN = ДРMN?
А) КМ — основа трикутника; Б) MP — основа трикутника;
B) КР — основа трикутника; Г) за будь-яких умов.
Достатній рівень навчальних досягнень A
7. На рисунку AD = DC, AB = СВ.
Доведіть, що 2DAB = ZDCB.
В
whunterto-67
8. На рисунку OB =OD, Z AOB = 2COD,
21 = 22. Знайдіть довжину відрізка ОС,
якщо AO+OB = 15 см, OD = 7 см.
В
2
D
Високий рівень навчальних досягнень
9. Відрізки АВ і СD перетинаються в точці О, яка є серединою відріз-
ка CD. Точки Bi C, AiD сполучені відрізками і 20CB = ZODA.
Через точку О проведено пряму, яка перетинає відрізки ВС і AD
уточках Ni M відповідно. Доведіть, що ON =OM.
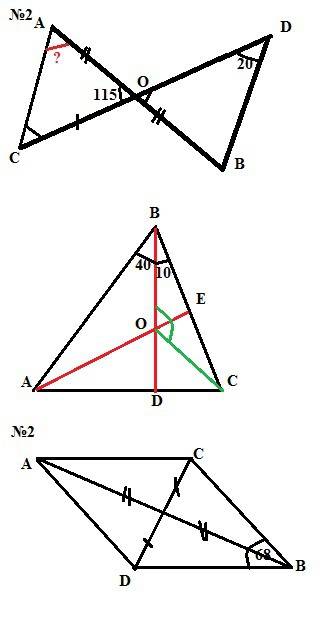
а) Докажите, что ΔАОС = ΔBOD.
б) Найдите ∠ОАС ,если ∠ОDB = 20°,∠АОС = 115°.
а) АО = ОС по условию,
ВO = OD по условию,
∠АОС = ∠BOD как вертикальные, ⇒
ΔАОС = ΔBOD по двум сторонам и углу между ними.
б) ∠ОСА = ∠ODB = 20°, так как в равных треугольниках напротив равных сторон лежат равные углы.
В ΔАОС: ∠ОАС = 180° - (∠АОС + ∠ОСА) = 180° - (115° + 20°) = 180° - 135° = 45°
№3) В равнобедренном треугольнике с периметром 64 см одна из сторон равна 16 см.
Найдите длину боковой стороны треугольника.
Формулировка "одна из сторон треугольника равна 16 см" предполагает, что будут рассмотрены два случая:
а) Пусть 16 см - основание равнобедренного треугольника.
Тогда боковая сторона равна
(64 - 16)/2 = 24 см
б) Боковая сторона 16 см не может быть равна, так как тогда основание равно
64 - 2 · 16 = 32 см, а любая сторона треугольника должна быть меньше суммы двух других.
№1) В треугольнике АВС высота ВD делит ∠В на два угла,причем ∠АВD = 40°, ∠СВD = 10°.
а) Докажите, что ΔАВС - равнобедренный, и укажите его основание.
б) Высоты данного треугольника пересекаются в точке О. Найдите ∠ВОС.
а) ∠АВС = ∠ABD + ∠CBD = 40° + 10° = 50°
В ΔBDA ∠BAD = 180° - 90° - 40° = 50°.
Так как ∠АВС = ∠ВАС, треугольник равнобедренный с основанием ВА.
б) ΔBCD: ∠BCD = 90° - ∠DBC = 90° - 10° = 80°.
В равнобедренном ΔАВС высота СН является так же и биссектрисой, значит ∠ВСО = ∠BCD/2 = 80°/2 = 40°.
ΔВСО: ∠ВОС = 180° - ∠ВСО - ∠СВО = 180° - 40° - 10° = 130°
№2 Отрезки АВ и СD пересекаются в точке О, которая является серединой каждого их них.
а) Докажите равенство треугольников АСВ и ВDА.
б) Найдите ∠АСВ,если ∠СВD = 68°.
а) АО = ОВ по условию,
BO = OD по условию,
∠АОС = ∠BOD как вертикальные, ⇒
ΔАОС = ΔBOD по двум сторонам и углу между ними, ⇒
АС = BD.
АО = ОВ по условию,
BO = OD по условию,
∠АОD = ∠BOC как вертикальные, ⇒
ΔАОD = ΔBOС по двум сторонам и углу между ними, ⇒
AD = ВС.
АС = BD,
AD = ВС,
АВ - общая сторона для треугольников АСВ и BDA, ⇒
ΔАСВ = ΔBDA по трем сторонам.
б) Из равенства треугольников
ΔАОС = ΔBOD равны углы, обозначенные цифрами 1 и цифрами 3.
Из равенства треугольников
ΔАОD = ΔBOС равны углы, обозначенные цифрами 2 и цифрами 4.
∠CBD = 68°, тогда в ΔCBD ∠3 + ∠4 = 180° - 68° = 112°.
∠АСВ = ∠3 + ∠4 = 112°
№3 Две стороны треугольника равны 0,9 см и 4,9 см. Найдите длину третьей стороны, если она выражается целым числом сантиметров.
Обозначим третью сторону а.
Любая сторона треугольника меньше суммы двух других его сторон:
0 < a < 5,8
0,9 < a + 4,9
4,9 < a + 0,9, ⇒ a > 4
Значит,
4 < a < 5,8.
На этот промежуток попадает только одно целое число: 5.
а = 5.