х=3+2у
5(3+2у)=4
15+10у=4
10у=4-15
10у=-11
у=-11/10
х=3-11/5
х=4/5
A)Допустим, это не так. Тогда точки A₁0₁B₁0₂ лежат в одной плоскости. Тогда в ней же лежат прямые, проходящие через O₁;O₂ параллельные A₁B₁ или, что то же самое, параллельные CD В частности, там лежат середины ребер AD и DD₁ ни вместе с A₁ задают плоскость грани куба AA₁D₁D, в которой не лежит B₁. Противоречие.
б)Введем координаты с началом в точке A и с осями x,y,z, направленными вдоль прямых AD,AB,AA₁ соответственно. Тогда координаты точек будут такими: A₁(0,0,2),B₁(0,2,2),O₁(1,1,0),O₂(2,1,1). Если отложить вектор A₁B₁ от точки B₁, то его конец T будет иметь координаты (1,3,0). Написав уравнение плоскости, проходящей через B₁,O₂,T, получим x+y+z-4=0. Тогда расстояние от точки (0;0;2) до этой плоскости составит 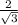
Объяснение:
выразим сначала x:\
x=3+2y
Подставим во второе равенство:
5(3+2y)+y=4
15+10y+y=4
11y=4-14
11y=-11
y=-1
Подставим y в первое равенство:
x-2*(-1)=3
x+2=3
x=1
ответ: x=1, y=-1