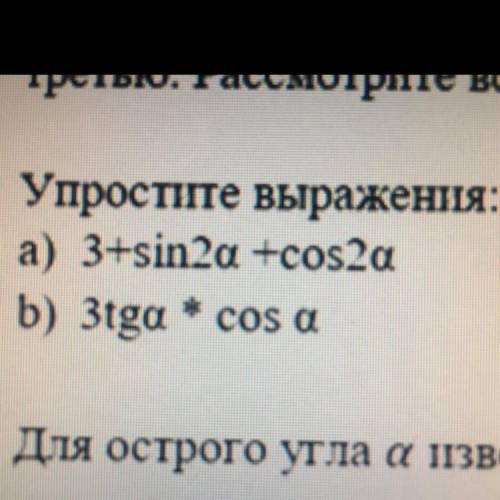
1. Сторона ромба равна 100:4=25 (см), так как все стороны у ромба равны.
2. Ромб диагоналями делится на 4 равных прямоугольных треугольника. Рассмотрим один из них.
Обозначим один катет через х см, тогда второй равен х+5 см. Используя теорему Пифагора, составляем уравнение:
х² + (х+5)² = 25²
х² + х² + 10х + 25 = 625
2х² + 10х - 600 = 0
Д=100+4800=4900
х1 = -20 - не подходит под условие задачи
х2 =15
15 см - один катет
15+5=20 (см) - второй катет
3. Каждая диагональ вдвое больше соответствующего катета.
d1 = 2·15 = 30 (см)
d2 = 2·20 = 40 (см)
ответ. 30 см, 40 см.
Сразу поправлю: часть круга, ограниченная дугой и её хордой называется сегментом.
Его площадь равна площади сектора минус площадь треугольника AOB.
обозначения: точка O -центр круга; точки A, B -концы хорды
H -длина хорды (как я понял, равна 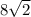 см)
см)
α -центральный угол AOB (для удобства в формулах)
Считать будем округлённо (если выразить ответ точно, то получится кучка дробей и радикалов).
В равнобедренном треугольнике AOB проведём высоту (пройдёт от точки O до центра хорды). Получим два прямоугольных треугольника- их гипотенуза равна радиусу круга, острый угол равен половине угла α. В прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к гипотенузе. Используя это, выразим и найдём радиус: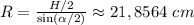
Найдём площадь сектора: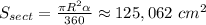
Найдём площадь равнобедренного треугольника AOB по формуле: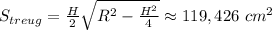
И, наконец найдём площадь сегмента: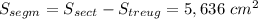
1)sin²a+cos²a=1 3+1=4
2)3sin