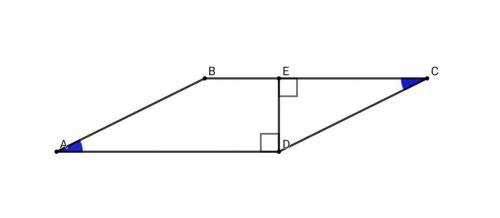
В четырёхугольнике ABCD по условию противолежащие стороны попарно равны ⇒ ABCD - параллелограмм
Противолежащие углы параллелограмма попарно равныУглы, прилежащие к любой стороне параллелограмма, в сумме равны 180°∠А + ∠В = 180°, ∠В = 180° - ∠A = 180° - 30° = 150° ⇒ ∠B = ∠D = 150°
∠ADE = ∠D - ∠CDE = 150° - 60° = 90°
Прямоугольная трапеция - это трапеция, боковая сторона которого перпендикулярна основаниямВЕ || AD, AB∦(не параллельно) ED, DE⊥BE, DE⊥AD ⇒ ABED - прямоугольная трапеция, что и требовалось доказать.
Дано:
ABCD - ромб
диагональ АС = 6√3 см
сторона ромба 6 см
Найти: углы ромба
Решение
Рассмотрим ΔАОВ. Он прямоугольный, так как диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам.
АВ = 6 см - гипотенуза ΔАОВ;
АО = АС:2 = (6√3) :2 = 3√3 см - катет рассматриваемого треугольника АОВ.
найдем второй катет ОВ.
ОВ²=АВ²-АО² = 6²- (3√3)² = 36-27=9
ОВ = √9 = 3 см.
Так как катет ОВ равен половине гипотенузы АВ, то напротив него лежит угол 30°. (∠ОАВ).
Соответственно, ∠АВО = 90-30 = 60°.
Так как диагонали ромба делят углы ромба пополам, несложно посчитать все углы ромба. Противоположные углы ромба равны.
∠DAB = ∠BCD = 30*2 = 60°
∠ADC = ∠ABC = 60*2 = 120°
ответ: углы ромба 60°, 60°, 120°, 120°.