Периметр одного треугольника , составляет 11/13 периметра подобного ему треугольника .разность двух соответственно сторон равна один метр .найдите большую из этих сторон!
Очень нечетко сформулированное условие. При пересечении трех прямых образуется 3 пары равных между собой вертикальных углов. Так как угол КАМ равен 90°, то значит прямые КL и MN взаимно перпендикулярны. Поэтому ∠KAN=∠LAN=∠MAL=∠KAM=90°. Условие "угол КАР: MAQ=4 : 5" дано для того, чтобы знать, как провести прямую PQ. ( cм. рис. 1) Если PQ проведена так как на рисунке 1, обозначим
∠KAP=4x; ∠MAQ=5x, тогда ∠KAQ=4x-90°;∠MAP=5x-90°; ∠KAQ+∠KAM+∠MAP=180°; 4x-90°+90°+5x-90°=180°. 9x=270° x=30° ∠KAP=4·30°=120°; ∠MAQ=5·30°=150°; значит ∠МАР=∠QAN=30°; ∠PАL=∠QAK=60° и ∠PАL:∠LАN=60°:90°=2:3 Условие "один из углов 80°" не выполняется.
Если прямая PQ расположена так как на рисунке 2. Аналогично случаю 1 обозначим ∠KAP=4x; ∠MAQ=5x, получаем невозможное∠KAP=4·30°=120°, а на рисунке угол ∠KAP- острый . Требуется дополнительное условие. Оно есть "один из углов 80°". Какой? Если ∠KAP=80°, тогда ∠MAQ=100° а на рисунке 2, угол ∠MAQ=180°-10°=170°.
Значит, нужен третий рисунок.
∠MAQ=80°,∠MAQ=5x. х=16° ∠KAP=4x=4·16°=64° Но тогда не выполняется условие "два других относятся как 2:3".
Треугольник равнобедренный, значит, углы при его основании равны (180º-120º):2=30º При вращении вокруг основания получится фигура в виде веретена, т.е. в виде двух равных конусов с общим основанием. Площадь такой фигуры равна боковой площади двух конусов с образующей, равной стороне заданного треугольника и радиусом, равным его высоте. Формула площади боковой поверхности конуса S=πrl, где r - радиус, l - образующая. Поскольку в задаче не даны длины сторон треугольника, примем длину его боковой стороны за а. Тогда высота треугольника - радиус тела вращения- как катет, противолежащий углу 30°, будет 0,5 а Sконуса=π*0,5a*a=π*0,5a² Площадь тела вращения вдвое больше. S=2*π*0,5a²=а²π(ед. площади) -------- Для таких задач обычно дается или длина боковой стороны треугольника. или длина его основания. Тогда, если задан равнобедренный треугольник с углом при вершине 120º, в ответе вместо а будет стоять численное выражение боковой стороны треугольника.
Т.к. треугольники подобны и их перметры относятся как 11/13, то и линейные размеры сходственных сторон также относятся как 11/13.
Пусть х м - дина меньшей сходственной стороны. Следовательно большая сторона равна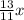 .
.
Тогда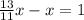
x=5,5 - меньшая
5,5+1=6,5-большая сторона