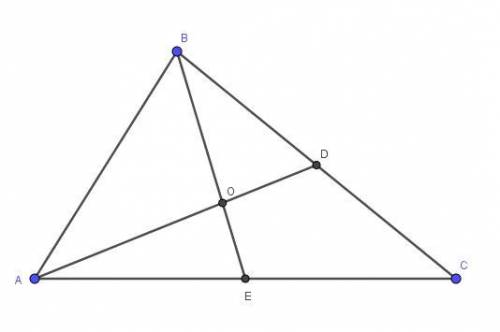
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть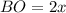 
см и 
см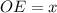, тогда 
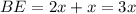, что по условию он равен 9 см.
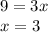
Следовательно,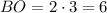 
см и 
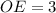см
Аналогично, пусть теперь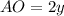 
см и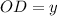 
, тогда 
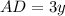и по условию равен 12 см
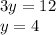
Таким образом,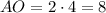 
см и 
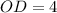см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника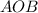 
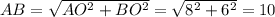см
По теореме Пифагора из прямоугольного треугольника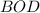 
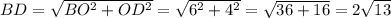см
Тогда 
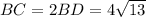см
Из прямоугольного треугольника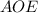 
по теореме Пифагора
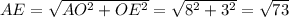см
Тогда 
см
ответ: 
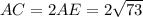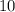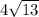см;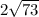 
см; 
см.
1. 4х+х=150
5х=150
х=30
ответ. 30°
2. х+х+2х=180
4х=180
х=45
ответ. 45°
3. 2х+3х=90
5х=90
х=18
3х-2х=х - разность.
ответ. 18°
4. Находим углы.
х+2х+3х=180
6х=180
х=30
30°,60°,90°.
Следовательно, данный треугольник - прямоугольный.
Меньшая сторона лежит против угла 30° и равна половине гипотенузы (гипотенуза, как большая сторона равна 8 см). Меньшая сторона равна 4 см.
Медиана, проведенная к гипотенузе, равна ее половине, т.е. 4 см.
Меньшая сторона + медиана, провед. к гипотенузе = 4+4 = 8 (см)
ответ. 8 см.
5. Так как треугольник равнобедренный, то высота, проведенная к основе (в данной задаче - это гипотенуза), является и медианой. А медиана, проведенная к гипотенузе, равна ее половине. Значит, гипотенуза равна двум медианам.
6·2=12 (см)
ответ. 12 см.
2.4см, 4.4см
Объяснение:
Образующийся тр-к BEC подобен AED, т.к. основы трапеции параллельны и соответственные углы при секущих боковых сторонах равны. Значит если х - 1 часть, то АЕ=5х+6х=11х, ВЕ/АЕ=6х/11х=6/11
ВС=y, тогда AD=y+2
Из подобия тр-ков получаем
BE/AE=BC/AD
6/11=y/(y+2)
11y=6y+12
5y=12
y=2.4
y+2=4.4