Плоскость параллельная оси цилиндра отсекает от окружности дугу длинной 4п см найдите расстояние секущей плоскости от оси цилиндра если радиус основания 6 см
Длина произвольной дуги: . Отсюда, после сокращения, находим: ,
Теперь рассмотрим треугольник, образованный двумя радиусами и углом AOB=360-240=120 градусов. Его высота, проведенная из вершины тупого угла, и будет искомым расстоянием.
По теореме косинусов находим высоту, которая и будет ответом.
Координаты середины отрезка ищутся как полусуммы соответствующих координат концов этого отрезка. Поэтому середина C_1 стороны AB имеет координаты (0;2), середина B_1 стороны AC - (1;0), середина A_1 стороны BC - (3;2). Будем искать уравнения медиан в виде y=kx+b (уравнение прямой с угловым коэффициентом). Подставляя в это уравнение координаты точек A и A_1. найдем уравнение медианы AA_1. Аналогично поступаем с медианами BB_1 и CC_1. В первом случае получаем систему уравнений относительно k и b 0= - 2k+b; 2=3k+b⇒k=2/5; b=4/5⇒ уравнение медианы AA_1 имеет вид y=2x/5+4/5 Аналогично получаем уравнения медианы BB_1: y=4x-4 и медианы CC_1: y= - x/2+2 (Если не правильно,не бейте..)
Длина произвольной дуги: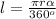
. Отсюда, после сокращения, находим:
,
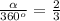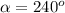
Теперь рассмотрим треугольник, образованный двумя радиусами и углом AOB=360-240=120 градусов. Его высота, проведенная из вершины тупого угла, и будет искомым расстоянием.
По теореме косинусов находим высоту, которая и будет ответом.