
Длина АВ=√(2-1)²+(3-6)²=√10
Длина ВС=АВ=√10 ( т.к квадрат)
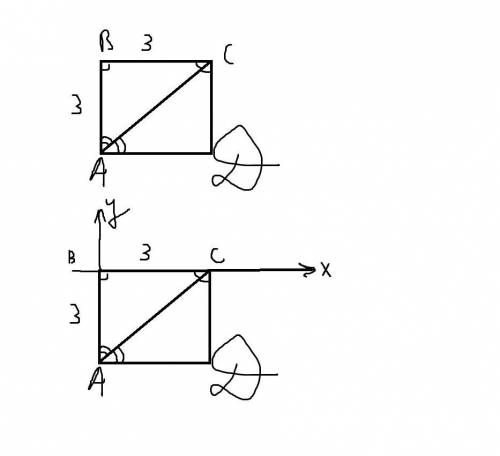
Координата "y" точки С такая же как и у вершины В ( на рисунок глянь)
Найдем координату х точки С:
ВС=√(х₂-х₁)²+(y₂-y₁)²
х₂; y₂- координата вершины С
х₁; y₁- координата вершины В
√10=√(х₂-2)²+(3-3)²
10=х₂-2⇒х₂=12
Координаты точки С (12;3)
Находим длину (модуль) вектора АС:
Координаты точки С (12;3)
Координаты точки А (1;6)
АС=√(х₂-х₁)²+(y₂-y₁)²
х₂; y₂- координата вершины С
х₁; y₁- координата вершины A
АС=√(х₂-х₁)²+(y₂-y₁)²=√(12-1)²+(3-6)²=√130
Координаты вектора АС:
АС ((х₂-х₁);(y₂-y₁))
АС(11;-3)
AB=12
tg30=x/12
x=12/корень из 3
S=2*S1+6*S2
S1=S3*6=((корень из 3 )*6^2/4)*6=54*корень из 3
S2=6*x=6*12/корень из 3
S=2* 54*корень из 3+ 6*6*12/корень из 3 =108*корень из 3 + 432/корень из 3