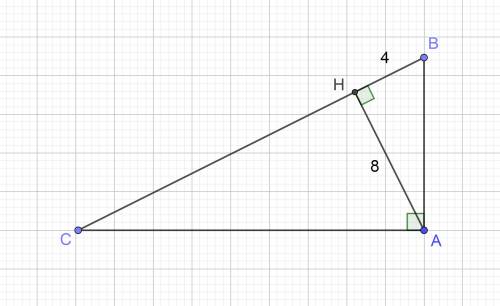
Задача: Найти площадь прямоугольного треугольника, в котором высота, опущенная из вершины прямого угла на гипотенузу, равна 8 см, и одна из проекций катета на гипотенузу равна 4 см.
Дан ΔABC, ∠C = 90°, CH = 8 см — высота, AH = 4 см — проекция катета AC.
Из определения, высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
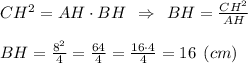
Тогда длина гипотенузы будет равна:
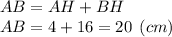
Подставим значения в формулу площади треугольника:
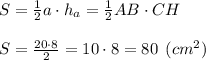
ответ: Площадь треугольника равна 80 см².
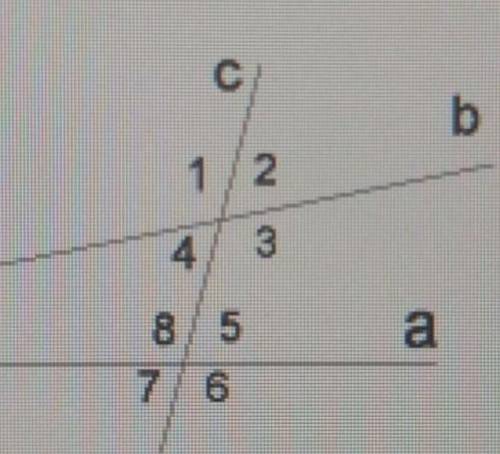
<1=160°
<2=20°
<3=160°
<4=20°
<5=130°
<6=50°
<7=130°
<8=50°
Объяснение:
<4=<2, вертикальные углы
<2=20°
<4+<3=180° смежные углы, отсюда
<3=180°-<4=180°-20°=160°
<3=<1, вертикальные углы.
<1=160°
<5=<7, вертикальные углы.
<7=130°
<5+<8=180°, смежные углы.
<8=180°-<5=180°-130°=50°
<8=<6, вертикальные углы.
Дано составлено не правильно, прямая а не параллельна прямой b.