Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.
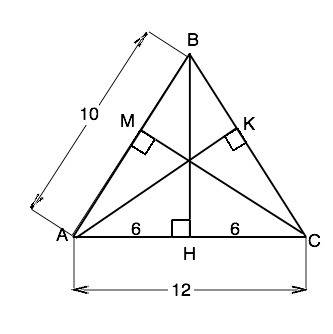
Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.

Здесь следует рассмотреть сечение шара плоскостью, которая делит и шар,и конус таким образом, что все мы наблюдаем как бы в срезе. Смотри рисунок. Используем расширенную теорему синусов, чтобы узнать радиус описанной окружности вокруг треугольника АВС. Заметим, что этот треугольник равнобедренный. АВравно ВС как образующие конуса. Найдем АВ по теореме Пифагора
AB=6 см.
Найдем противолежащий угол ВСА. Он равен углу ВАС.
По теореме синусов нам нужен синус этого угла.
По теореме синусов
2R=12
R=6 - радиус описанной окружности вокруг треугольника АВС, и радиус шара описанного вокруг конуса одновременно.
Объем шара находится по стандартной формуле