они действительно равны
Объяснение:
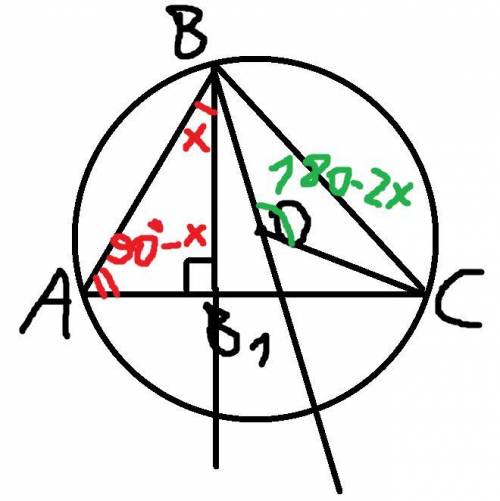
Пусть <ABB1 = x, тогда если <BB1A = 90 градусов (т.к. BB1 - высота), то ABB1 = (180 - 90 - x) градусов = (90 - x) градусов. Т.к. <BAC - вписанный для дуги BC, а <BOC - центральный для этой же дуги BC, то <BOC = 2*<BAC = 2*(90 - x)градусов = (180 - 2x) градусов. Очевидно, что BO = OC = R, тогда треугольник BOC - равнобедренный, тогда <CBO = <BCO = (180 - < BOC) / 2 = (180 - (180 - 2x)) / 2 = 2x / 2 = x. Следовательно <ABB1 = <CBO = x.
Пусть данная пирамида АВСДS (S - вершина, SO - высота) О - точка пересечения диагоналей квадрата АВСД.
Диагональ квадрата АС равна 24корня из 2х. (есть такое свойство)))
ОД=12 корня из 2х.
Из треуг. SОД (угол О=90) по т. Пифагора: SD=квадратный корень из выражения (256+144*2)=4корня из 34.
SD - это было расстояние от вершины пирамиды до вершины основания.
А до сторон:
Проведём ОК перпендикулярно АД. Соеденим S и К, SK искомое расстояние от вершины пирамиды до сторон основания.
ОК - радиус вписанной окружности в АВСД, ОК=24/2=12см.
Из треуг. SОК (угол О=90 град.) по т. Пифагора: SK= корень из выражения (256+144) = 20 см.