
Объяснение:
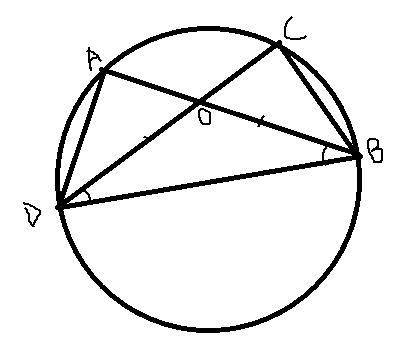
Дано: Хорды AB=CD пересекаются в точке О. Доказать: AO=CO, DO=BO.
Док-во: Соединим точки A B C D как на рисунке и рассмотрим треугольники ABD и CDB. Равные хорды стягивают равные дуги, значит вписанные углы ADB и CBD равны, а вписанные углы DAB и BCD опираются на одну и ту же дугу, значит они равны. Поскольку в треугольнике сумма углов равна 180°, то и оставшиеся углы ABD и CDB равны. Из равенства этих двух углов (<ABD=<CDB) следует, что △DOB - равнобедренный. => DO=BO. Поскольку AB=AO+BO и CD=DO+CO, а AB=CD, то и AO=CO, чтд.
Теорема косинусов для треугольника AМC
AC^2=AM^2+MC^2-2*AM*CM*cosAMC
Теорема косинусов для треугольника BМC
BC^2=BM^2+MC^2-2*BM*CM*cosBMC
AC=BC (треугольник равносторонний) Тогда AC^2=BC^2
AM^2+MC^2-2*AM*CM*cosAMC=BM^2+MC^2-2*BM*CM*cosBMC
AM^2-2*AM*CM*cosAMC=BM^2-2*BM*CM*cosBMC
АМ и ВM знаем
2^2-2*2*CM*cosAMC=10^2-2*10*CM*cosBMC
4-4*CM*cosAMC=100-20*CM*cosBMC
Углы ВМС и ВАС равны, опираются на одну дугу. ВАС=60 - равносторонний треугольник.
Угол АМС=АМВ+ВМС=АСВ+ВАС=60+60=120
4-4*CM*cos120=100-20*CM*cos60
4-4*CM*(-1/2)=100-20*CM*1/2
4+2*CM=100-10*CM
12*CM=96
СМ=8
ответ: 8