AD = (√21)/5 ед.
Объяснение:
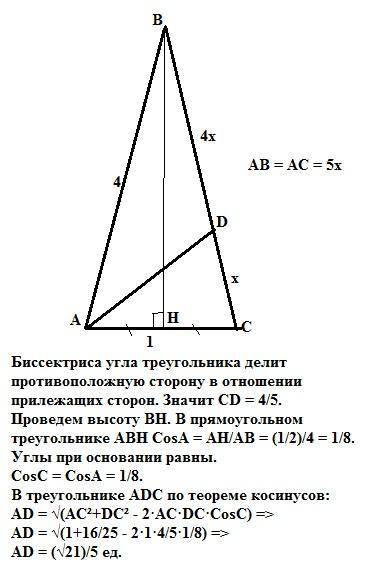
Биссектриса AD угла А треугольника АВС делит противоположную сторонуВС в отношении прилежащих сторон.
То есть BD/DC = 4/1. ВС =АВ = 4 ед.
Значит СD = 4/5 ед.
Проведем высоту ВН. В равнобедренном треугольнике АВС высота является и медианой. АН = НС = 1/2 ед.
В прямоугольном треугольнике АВН
CosA = AH/AB = (1/2)/4 = 1/8.
Углы при основании равнобедренного треугольника равны.
CosC = CosA = 1/8.
В треугольнике ADC по теореме косинусов:
AD = √(AC²+DC² - 2·AC·DC·CosC) =>
AD = √(1+16/25 - 2·1·4/5·1/8) => AD = √(21/25).
AD = (√21)/5 ед.
Из теоремы о пересекающихся хордах следует: произведение отрезков хорды АВ равно произведению отрезков хорды CD. ⇒
AE•BE=CE•DE
Примем коэффициент отношения отрезков хорды CD за х.
Тогда 3•36=3a•4a
12a²=108
a=√9=3
СD=3a+4a=9+12=21 (ед. длины)
Диаметр = 2R - наибольшая хорда окружности. Поэтому наименьшим диаметром данной окружности может быть хорда АВ, и тогда наименьший радиус равен ее половине.
R=(3+36):2=19,5 (ед. длины)