Всего бочек 21, значит каждому купцу в сумме должно достаться по 7 бочек
Теперь делим сам мёд:
Пусть половина бочки это одна доля. Тогда в полных бочках содержится 14 долей, а в полупустых 7 долей, всего 21 доля, из которых каждому купцу должно достаться по 7 долей. Исходя из этого, бочки следует распределить следующим образом:
1 купец: 3 полных бочки, 1 полупустая, 3 пустых. Всего бочек - 7, мёда - 3,5 бочки.
2 купец: 2 полных бочки, 3 полупустых, 2 пустых. Всего бочек - 7, мёда - 3,5 бочки.
3 купец: 2 полных бочки, 3 полупустых, 2 пустых. Всего бочек - 7, мёда - 3,5 бочки.
Сечением будет равнобедренная трапеция, т.к. основания призмы лежат в параллельных плоскостях, то секущая плоскость их будет пересекать по параллельным прямым.
Пусть К и М середины рёбер АС и ВС, тогда МК средняя линия, по свойству она параллельна третьей стороне АВ и равна её половине - 4 см (стороны основания равны по 8см)
Секущая плоскость проходит через точку А1 и параллельна МК, т.е. совпадает с А1В1 (МК II АВ II А1В1). А1В1МК - трапеция с основаниями А1В1=8см и МК=4см
Боковые стороны равны из равенства прямоугольных треугольников АА1К и ВВ1М (по двум катетам). А1К и В1М - гипотенузы этих треугольников. Их находим по теореме Пифагора √3²+4²=√9+16=√25=5см.
Р=4+8+2·5=22см
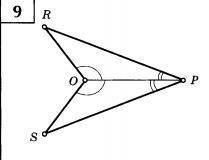
ROP = SOP
угол ROP равен углу SOP
угол RPO равен углу SPO
OP общая
2 признак равенства треугольников