Рассмотрим один из двух треугольников, полученных при проведении диагонали в боковой грани параллелепипеда:
Треугольник прямоугольный т.к. параллелепипед прямой, по этой же причине один из острых углов равен 30°; гипотенуза (диагональ боковой грани) равна 8см; катет лежащий напротив угла в 30° (боковое ребро) равен половине гипотенузы: 8см:2 = 4см; другой катет (сторона основания), по теореме Пифагора, равен √(8²-4²) = √(64-16) = √48 см.
Объём параллелепипеда можно найти через его высоту (в нашем случаи это и боковое ребро) и площадь основания. В основании лежит квадрат, поэтому его площадь равна (√48 см)² = 48 см².
Тогда объём равен 4см · 48см² = 192 см³
ответ: 192см³.
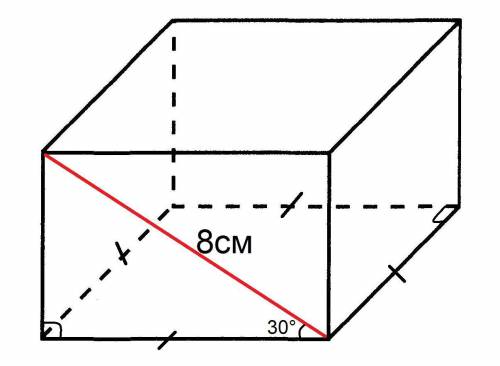
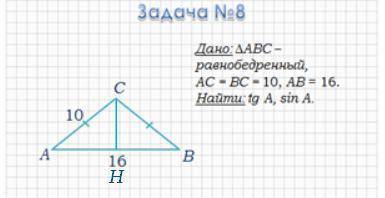
Задача: Дан ΔABC — равнобедренный, AC = BC = 10, AB = 16. Найти tg A, sin A.
Проведем высоту CH в ΔABC к стороне AB. Образуется два равных треугольника, т.к. ΔABC равнобедренный. AH = HB = 16/2 = 8.
Р-м ΔACH:
∠AHC = 90°, т.к CH — перпендикуляр к AH (AH∈AB) ⇒ ΔACH — прямоугольный.
Синус угла равен отношению противолежащего катета к гипотенузе.
Найдем катет CH за т. Пифагора:
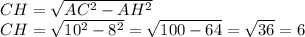
Тогда синус ∠A будет равен:
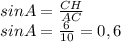
Тангенс угла равен отношению противолежащего катета к прилежащему:
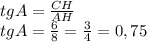
ответ: tg A = 0,75; sin A = 0,6.
1)
Опускаешь из точки О высоту ОД на сторону МN.
Треугольники МОД и МОК - равны.
ОД - искомое расстояние.
ОД=ОК = 9 см
2)
угол А=60гр.
угол В=90гр.
АС+АВ=28.2см. (т.к. против меньшего из углов лежит меньшая из сторон)
АС-?
1. угол С=90-60=30гр.
2. по свойству прямоугольного треугольника известно, что катет, лежащий против угла в 30 градусов, равен половине гипотинузы.
3. пусть AB=х, тогда АС=2х
2х+х=28.2
3х=28.2
х=9.4 см. (АВ)
4. АС=9.4*2=18.8 см.
ответ: 18.8 см.