Медиана делит основание треугольника на две равные части,поэтому треугольники АВК и ВКС равны между собой по третьему признаку равенства треугольников-если три стороны одного треугольника равны трём сторонам другого треугольника,то эти треугольники равны между собой
АВ=ВС,как стороны равнобедреного треугольника
АК=КС ,сторону АС медиана поделила на две равных стороны
И ВК-общая сторона
Периметр АВС
АВ+ВС+АК+КС=36 см
Периметры двух треугольников АВК и ВКС равны
АВ+ВС+АК+КС+(ВК)+(ВК)+30+30=60 см
(60-36);2=24:2=12 см
Объяснение:
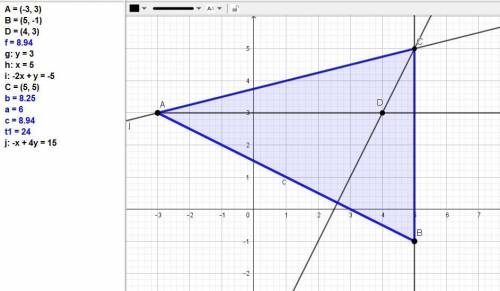
Уравнение АВ: (x-(-3))/(5-(-3) = (y-3)/(-1-3) или (x + 3)/8 = (y - 3)/(-4).
В общем виде x + 2y - 3 = 0.
Так как высота АД - горизонтальная линия, то уравнение стороны ВС:
х = 5.
В уравнении высоты СД как перпендикуляра к АВ коэффициенты А и В меняются на -В и А (скалярное произведение равно 0).
Уравнение СД: -2х + у + С = 0. Подставим координаты точки Д, через которую проходит высота: -2*4 + 1*3 + С = 0, отсюда С = 8-3 = 5.
Уравнение СД: -2х + у + 5 = 0.
Находим координаты точки С как точки пересечения стороны ВС и высоты СД:
{x = 5,
{-2х + у + 5 = 0, подставим х = 5.
-2*5 + у + 5 = 0, у = 10 - 5 = 5.
Точка С(5;5).
Уравнение АС: (x-(-3))/(5-(-3) = (y-3)/(5-3) или (x + 3)/8 = (y - 3)/2.
В общем виде x - 4y + 15 = 0.
Трапеция АВСД. АВ=СД=ВС, уголА=уголД. проводим высоты ВН=СК на АД, точка О пересечение ВН и АС. ВО=15, НО=12,
Треугольник АВС равнобедренный АВ=ВС, угол ВАС=уголВСА , угол САД=уголАСВ как внутренние разносторонние, диагональ АС - биссектриса угла А
АВ =а, ВО/НО=АВ/АН (свойства биссектрисы), 15/12 = а /АН
АН = 4/5 х а
треугольник АВН. ВН = корень (АВ в кввадрате - АН в квадрате) =
=корень (а в квадрате - 16/25 х а в квадрате) =3/5 х а
ВН=ВО+НО=15+12=27 = 3/5 х а, а = 27 х 5 /3=45 = ВС=СД
треугольники АВН=треугольнику КСД, по гипотенузе и острому углу, АН=КД = 4/5 х 45 = 36, НК=ВС=45, АД=36+45+36=117
Площадь = (АД+ВС)/2 х ВН = (117+45)/2 х 27 = 2187