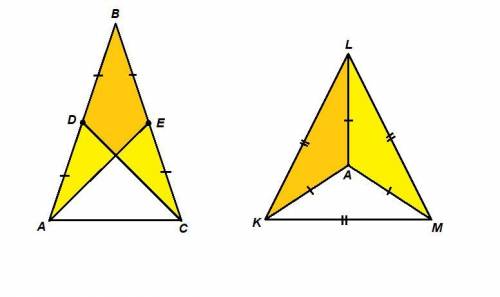
1) Дано: ΔАВС, D - середина АВ, Е - середина ВС, AD = CE.
Доказать: ΔBDC = ΔBEA.
Доказательство:
AD = DB, так как D - середина АВ,
СЕ = ЕВ, так как Е - середина ВС,
AD = CE по условию, значит
AD = DB = СЕ = ЕВ, а следовательно
АВ = ВС.
В треугольниках BDC и BEA:
ВС = АВ,
DB = EB,
∠B - общий, ⇒
ΔBDC = ΔBEA по двум сторонам и углу между ними.
2) Дано: ΔKLM - равносторонний, А - внутренняя точка ΔKLM,
AK = AL = AM.
Доказать: ΔKLA = ΔMLA.
Доказательство:
АК = АМ по условию,
LK = LM как стороны равностороннего треугольника,
AL - общая сторона для треугольников KLA и MLA, ⇒
ΔKLA = ΔMLA по трем сторонам.
Из вершины А, как из центра, откладываем циркулем равные отрезки АЕ и АО на сторонах АВ и АС.. Из точек О и Е проводим полуокружности равным радиусом больше половины ЕО.
Точки пересечения окружностей по обе стороны ЕО соединяем прямой до пересечения с ВС в точкой К. АК - срединный перпендикуляр равнобедренного треугольника АОЕ. Следовательно, он - биссектриса.
АК-биссектриса угла А.
---
2) Медиана ВМ.
Для ее построения нужно найти середину стороны ВС, для чего из В и С чертим полуокружности радиусом больше половины ВС и точки их пересечения по обе стороны соединяем. Точка М пересечения этого отрезка и стороны ВС - середина ВС.
ВМ - медиана.
3) Высота СН
Из вершины С как из центра раствором циркуля, равным стороне СВ, делаем насечку на стороне АВ. Из этой точки и точки В как их центров раствором циркуля с одинаковым радиусом строим полуокружности.
Соединяем отрезком точки их пересечения по обе стороны от АВ.
Пересечение этого отрезка с АВ - основание Н высоты СН.
Соединим С и Н.
СН - высота треугольника АВС.