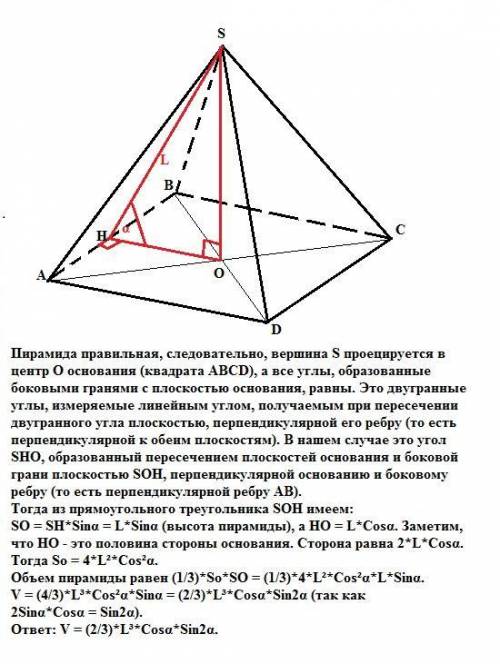
Пирамида правильная, следовательно, вершина S проецируется в центр О основания (квадрата АВСD), а все углы, образованные боковыми гранями с плоскостью основания, равны. Это двугранные углы, измеряемые линейным углом, получаемым при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям). В нашем случае это угол SHO, образованный пересечением плоскостей основания и боковой грани плоскостью SOH, перпендикулярной основанию и боковому ребру (то есть перпендикулярной ребру АВ).
Тогда из прямоугольного треугольника SOH имеем:
SO = SH*Sinα = L*Sinα (высота пирамиды), а НО = L*Соsα.
Заметим, что НО - это половина стороны основания. Сторона равна 2*L*Соsα.
Тогда площадь основания So = 4*L²*Соs²α.
Объем пирамиды равен (1/3)*So*SO = (1/3)*4*L²*Соs²α*L*Sinα.
V = (4/3)*L³*Соs²α*Sinα = (2/3)*L³*Соsα*Sin2α (так как
2Sinα*Cosα = Sin2α).
ответ: V = (2/3)*L³*Соsα*Sin2α.
теперь тебе надо представить половину осевого сечения этого конуса...это будет прямоугольная трапеция где основания это радиусы r и R одна боковая сторона=высоте трапеции =6,3 дм вторая сторона (большая) это образующая конуса=6,5дм
проведём из тупого угла высоту и найдём кусок который она отсекает от большего основания (то есть от R)
этот кусок=v(6,5^2-6,3^2)=v(42,25-39,69)=v2,56=1,6 дм
теперь r+R запишем как r+r+1,6 имеем
r+r+1,6=4
2r=4-1,6
2r=2,4
r=1,2 дм маленький радиус
R=r+1,6=1,2+1,6=2,8 дм большой радиус