по т синусов найдем стороны треугольника
ВС=1,73*0,77:0,86=1,55
АС=0,94*1,73:0,86=1,89
S=0,5*1,73* 1,55 *0,94=1,26
R=(1.73*1.55*1.89)/(4*1.26)=5.07/5.04=1.006
d=2*1.006=2,012
Объяснение:
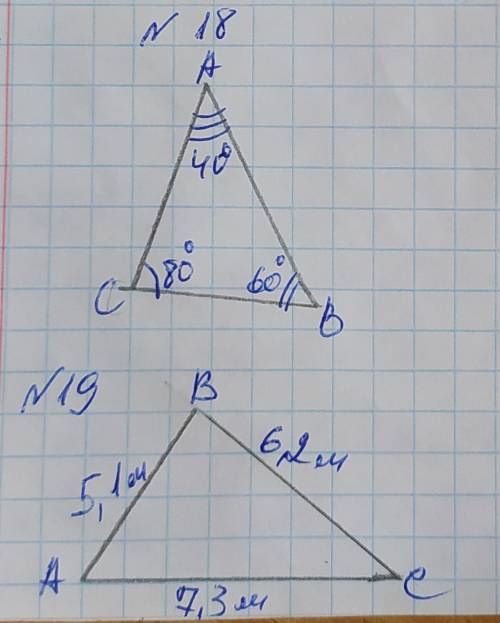
№18
ДАНО: ∆АВС, ∠А=40°, ∠В=60°, ∠С=80°.
НАЙТИ: наибольшую сторону.
Напротив большего угла лежит наибольшая сторона, поэтому наибольшей стороной является АВ, так как она лежит напротив ∠С=80°, а меньшей стороной является ВС, так она лежит напротив меньшего ∠А=40°
№19
ДАНО:
∆АВС, АВ=4,1м; ВС=6,2м; АС=7,3см
НАЙТИ: наибольший и наименьший углы.
Больший угол лежит напротив большей стороны и меньший угол лежит напротив меньшей стороны, поэтому большим углом является ∠В, так как он лежит напротив большей стороны АС=7,3м, а меньшим углом является ∠С, так как лежит напротив меньшей стороны АВ=5,1м
V = 24π см³.
Объяснение:
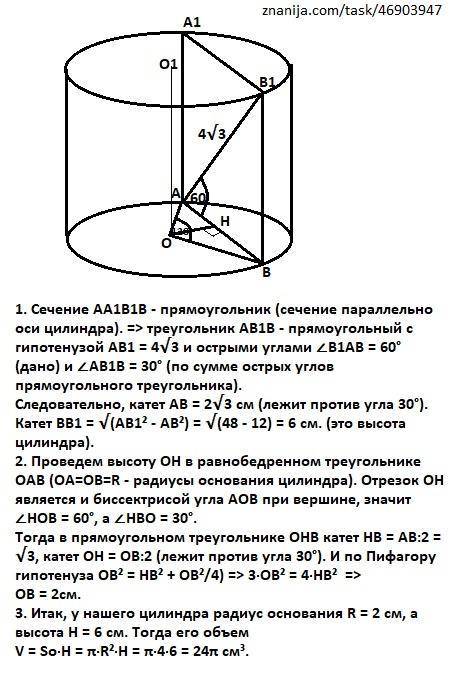
1. Сечение АА1В1В - прямоугольник (сечение параллельно оси цилиндра). => треугольник АВ1В - прямоугольный с гипотенузой АВ1 = 4√3 и острыми углами ∠В1АВ = 60° (дано) и ∠АВ1В = 30° (по сумме острых углов прямоугольного треугольника).
Следовательно, катет АВ = 2√3 см (лежит против угла 30°).
Катет ВВ1 = √(АВ1² - АВ²) = √(48 - 12) = 6 см. (это высота цилиндра).
2. Проведем высоту ОН в равнобедренном треугольнике ОАВ (ОА=ОВ=R - радиусы основания цилиндра). Отрезок ОН является и биссектрисой угла АОВ при вершине, значит ∠НОВ = 60°, а ∠НВО = 30°.
Тогда в прямоугольном треугольнике ОНВ катет НВ = АВ:2 = √3, катет ОН = ОВ:2 (лежит против угла 30°). И по Пифагору гипотенуза ОВ² = НВ² + ОВ²/4) => 3·ОВ² = 4·НВ² =>
ОВ = 2см.
3. Итак, у нашего цилиндра радиус основания R = 2 см, а высота Н = 6 см. Тогда его объем
V = So·H = π·R²·H = π·4·6 = 24π см³.
Найти диаметр окружности, описаной около треугольника ABC,
если AB=√3 см, угол B=70°, угол A=50°
По теореме синусов, отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности=2R
Найдем третий угол, против которого лежит известная сторона треугольника.
Так как сумма углов треугольника равна 180°,
угол С=180°-50°-70°=60°.
АВ:sin(60°)=(√3:√3)·2=2
2R=2 =D
ответ: диаметр описанной окружности равен 2см.